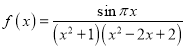题目内容
【题目】已知函数![]() .其中
.其中![]()
(1)求![]() 的单调区间;
的单调区间;
(2)当![]() 时,
时,![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]()
【解析】
(1)对![]() 求导得
求导得![]() ,按
,按![]() ,
,![]() ,
,![]() 分类讨论
分类讨论![]() 的正负,即可得
的正负,即可得![]() 的单调区间;
的单调区间;
(2)由![]() 及(1)知,当
及(1)知,当![]() 时,不合题意;当
时,不合题意;当![]() 时,
时,![]() 恒成立,由
恒成立,由![]() ,得
,得![]() ,要使
,要使![]() ,则当
,则当![]() 时,
时,![]() 恒成立,解出
恒成立,解出![]() 的取值范围即可.
的取值范围即可.
(1)![]()
①当![]() 时,
时,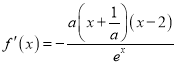 ,令
,令![]() ,解得
,解得![]() ,
,![]() ,且
,且![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以,![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() 和
和![]() ;
;
②当![]() 时,
时,![]() ,所以,
,所以,![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ;
;
③当![]() 时,令
时,令![]() ,解得
,解得![]() ,
,![]() ,并且
,并且![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以![]() 的单调递增区间是
的单调递增区间是![]() 和
和![]() ,单调递减区间是
,单调递减区间是![]() ;
;
综上:当![]() 时,
时,![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() 和
和![]() ;
;
当![]() 时,
时,![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ;
;
当![]() 时,
时,![]() 的单调递增区间是
的单调递增区间是![]() 和
和![]() ,单调递减区间是
,单调递减区间是![]() .
.
(2)由![]() 及(1)知,
及(1)知,
①当![]() 时,
时,![]() ,不恒成立,因此不合题意;
,不恒成立,因此不合题意;
②当![]() 时,
时,![]() 的单调递增区间是
的单调递增区间是![]() 和
和![]() ,单调递减区间是
,单调递减区间是![]() .
.
![]() ,得
,得![]() ,
,![]() ,
,
当![]() 时,要使
时,要使![]() ,则当
,则当![]() 时,
时,![]() 恒成立,
恒成立,
即![]() ,故
,故![]() ,所以
,所以![]() .
.

【题目】某同学用“随机模拟方法”计算曲线![]() 与直线
与直线![]() 所围成的曲边三角形的面积时,用计算机分别产生了10个在区间[1,e]上的均匀随机数xi和10个在区间[0,1]上的均匀随机数
所围成的曲边三角形的面积时,用计算机分别产生了10个在区间[1,e]上的均匀随机数xi和10个在区间[0,1]上的均匀随机数![]()
![]() ,其数据如下表的前两行.
,其数据如下表的前两行.
x | 2.50 | 1.01 | 1.90 | 1.22 | 2.52 | 2.17 | 1.89 | 1.96 | 1.36 | 2.22 |
y | 0.84 | 0.25 | 0.98 | 0.15 | 0.01 | 0.60 | 0.59 | 0.88 | 0.84 | 0.10 |
lnx | 0.90 | 0.01 | 0.64 | 0.20 | 0.92 | 0.77 | 0.64 | 0.67 | 0.31 | 0.80 |
由此可得这个曲边三角形面积的一个近似值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【题目】某校为提高课堂教学效果,最近立项了市级课题《高效课堂教学模式及其运用》,其中王老师是该课题的主研人之一,为获得第一手数据,她分别在甲、乙两个平行班采用“传统教学”和“高效课堂”两种不同的教学模式进行教学实验.为了解教改实效,期中考试后,分别从两个班级中各随机抽取![]() 名学生的成绩进行统计,作出如图所示的茎叶图,成绩大于
名学生的成绩进行统计,作出如图所示的茎叶图,成绩大于![]() 分为“成绩优良”.
分为“成绩优良”.
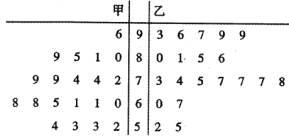
(1)由以上统计数据填写下面![]() 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过![]() 的前提下认为“成绩优良与教学方式有关”?
的前提下认为“成绩优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
(2)从甲、乙两班![]() 个样本中,成绩在
个样本中,成绩在![]() 分以下(不含
分以下(不含![]() 分)的学生中任意选取
分)的学生中任意选取![]() 人,求这
人,求这![]() 人来自不同班级的概率.
人来自不同班级的概率.
附: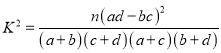 ,其中
,其中![]() )
)
|
|
|
|
|
|
|
|
|
|
|
|
|
|