题目内容
【题目】已知函数f(x)=lg(x+1),g(x)=lg(1﹣x). (Ⅰ)求函数f(x)+g(x)的定义域;
(Ⅱ)判断函数f(x)+g(x)的奇偶性,并说明理由;
(Ⅲ)判断函数f(x)+g(x)在区间(0,1)上的单调性,并加以证明.
【答案】解:(Ⅰ)要函数有意义,则 ![]() ∴﹣1<x<1,
∴﹣1<x<1,
即函数的定义域为(﹣1,1)
(Ⅱ)解:令F(x)=f(x)+g(x)=lg(x+1)+lg(1﹣x)=lg(1﹣x2).
由(1)得函数定义域关于原点对称
又F(﹣x)=F(x),
∴函数F (x)是偶函数.
(Ⅲ)解:F(x)=f(x)+g(x)在区间(0,1)上是减函数,
理由如下:
设x1、x2∈(0,1),x1<x2 ,
则 ![]() ,即
,即 ![]() >1,
>1,
∴F (x1)﹣F(x2)=lg(1﹣x12)﹣lg(1﹣x22)=lg ![]() >0.
>0.
即F (x1)>F(x2)
∴F(x)=f(x)+g(x)在区间(0,1)上是减函数
【解析】(Ⅰ)由 ![]() 可得函数f(x)+g(x)的定义域;(Ⅱ)根据F(﹣x)=F(x),可得:函数F (x)是偶函数(Ⅲ)F(x)=f(x)+g(x)在区间(0,1)上是减函数,作差可证明结论.
可得函数f(x)+g(x)的定义域;(Ⅱ)根据F(﹣x)=F(x),可得:函数F (x)是偶函数(Ⅲ)F(x)=f(x)+g(x)在区间(0,1)上是减函数,作差可证明结论.
【考点精析】解答此题的关键在于理解复合函数单调性的判断方法的相关知识,掌握复合函数f[g(x)]的单调性与构成它的函数u=g(x),y=f(u)的单调性密切相关,其规律:“同增异减”.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案【题目】某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如表:
API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
(1)若某企业每天由空气污染造成的经济损失S(单位:元)与空气质量指数API(记为ω)的关系式为: S= 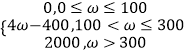 ,试估计在本年内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
,试估计在本年内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
(2)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面2×2列联表,并判断能否有95%的把握认为该市本年空气重度污染与供暖有关? 附:
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
k2= ![]()
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |