题目内容
所有正奇数如下数表排列(表中下一行中的数的个数是上一行中数的个数的2倍)
第一行 1
第二行 3 5
第三行 7 9 11 13
... ...
则第6行中的第3个数是 .
第一行 1
第二行 3 5
第三行 7 9 11 13
... ...
则第6行中的第3个数是 .
67
解:根据题意,分析数表可得,表中的数从上到下,每行从左到右依次为1、3、5、7、…;
是一个首项为1,公差为2的等差数列,设为{an},则其通项为an=2n-1;
而表中下一行中的数的个数是上一行中数的个数的2倍,且第1行有1个数,
则前5行有1+2+4+8+16=31个数,则第6行中的第3个数为这个数列的第34个数,
即{an}这个数列的第34项,易得an=2n-1=2×34-1=67;
故答案为67
是一个首项为1,公差为2的等差数列,设为{an},则其通项为an=2n-1;
而表中下一行中的数的个数是上一行中数的个数的2倍,且第1行有1个数,
则前5行有1+2+4+8+16=31个数,则第6行中的第3个数为这个数列的第34个数,
即{an}这个数列的第34项,易得an=2n-1=2×34-1=67;
故答案为67

练习册系列答案
相关题目
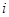 行里的最后一个数字是多少?
行里的最后一个数字是多少? 中得出的一般性结论是_____________.
中得出的一般性结论是_____________.
 ,则
,则 ”类比推出“若
”类比推出“若 ,则
,则 ”类比推出“
”类比推出“ ”
” (c≠0)”
(c≠0)” ” 类比推出“
” 类比推出“ ”
”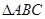 中,
中,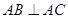 ,点
,点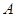 在
在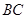 边上的射影为
边上的射影为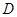 ,有
,有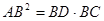 .”类比平面几何定理,研究三棱锥的侧面面积与射影面积、底面面积的关系,可以得出的正确结论是:“在三棱锥
.”类比平面几何定理,研究三棱锥的侧面面积与射影面积、底面面积的关系,可以得出的正确结论是:“在三棱锥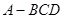 中,
中,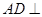 平面
平面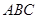 ,点
,点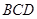 上的射影为
上的射影为 ,则有 .”
,则有 .”
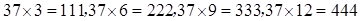 ,....
,.... 