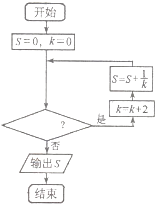
题目内容
【题目】数列{an}的前n项和为Sn=2an﹣2，数列{bn}是首项为a1 ， 公差不为零的等差数列，且b1 ， b3 ， b11成等比数列．
（1）求数列{an}与{bn}的通项公式；
（2）设数列{cn}满足cn= 
，前n项和为Pn ， 对于n∈N*不等式 Pn＜t恒成立，求实数t的取值范围．
【答案】
（1）解：当n=1时，a1=S1=2a1﹣2，a1=2，
当n≥2时，an=Sn﹣Sn﹣1=（2an﹣2）﹣（2an﹣1﹣2）=2an﹣2an﹣1，
得an=2an﹣1，
∴数列{an}是以2为首项，公比为2的等比数列，
∴数列{an}的通项公式为an=2n．
则b1=a1=2，设公差为d，则b1，b3，b11成等比数列，
得（2+2d）2=2×（2+10d），
解得d=0（舍去）或d=3
∴数列{bn}的通项公式为bn=3n﹣1
（2）解：cn= 
= 
= 
（ 
﹣ 
）
则pn= （ 
+…+ - ）= （ 
） 
，
又对于n∈N*不等式 Pn＜t恒成立，
所以实数t的取值范围是t≥ 
【解析】（1）根据当n=1时a1=S1 ， 当n≥2时an=Sn﹣Sn﹣1 ， 判断出数列{an}是以2为首项，公比为2的等比数列，并求出
an ， 由等比中项的性质、等差数列的通项公式求出bn；（2）由（1）和题意求出cn ， 利用裂项相消法求出前n项和Pn ， 化简后求出Pn的范围，由恒成立求出实数t的取值范围．
【考点精析】认真审题，首先需要了解等比数列的通项公式（及其变式）(通项公式：
)，还要掌握数列的前n项和(数列{an}的前n项和sn与通项an的关系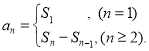
)的相关知识才是答题的关键．
【题目】有甲、乙两个班级进行数学考试，按照大于或等于90分为优秀，90分以下为非优秀统计成绩后，得到如表的列联表．
优秀 | 非优秀 | 总计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 100 |
已知在全部100人中抽到随机抽取1人为优秀的概率为 
．
（1）请完成如表的列联表；
（2）根据列联表的数据，有多大的把握认为“成绩与班级有关系“？
（3）按分层抽样的方法，从优秀学生中抽出6名组成一个样本，再从样本中抽出2名学生，求恰好有1个学生在甲班的概率．
参考公式和数据：K2= 
，其中n=a+b+c+d．
下面的临界值表供参考：
p（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
