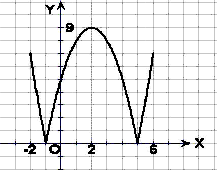
题目内容
| |||||||||||||||
答案:
解析:
解析:
(1) |
|
(2) |
方程
由于 |
(3) |
解法一:当
①当
则 ②当 由①、②可知,当 因此,在区间 解法二:当 由 令 在区间 如图可知,由于直线 |

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
| |||||||||||