题目内容
设集合M={(x,y)|x2+y2=1,x∈R, y∈R},N={(x,y)|x2-y=0,x∈R,y∈R},则集合M∩N中元素的个数为( )A.1 B.2 C.3 D.4
B?
解析:集合A表示以原点为圆心,半径为1的圆,集合B表示抛物线,求M∩N中元素的个数即求两条曲线的交点个数.由
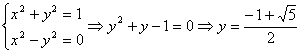 .
.
∵y=x2,y≥0,
∴y= ![]() .?
.?
∴x2= ![]() .?
.?
故方程组有两组解,M∩N中元素的个数为2,选B.

练习册系列答案
相关题目
设集合M={x|y=
},N={y|y=-x2+1,x∈R},则M∩N=( )
| 4-x2 |
| A、? | B、[-2,2] |
| C、[-2,1] | D、[0,1] |