题目内容
设函数f(x)=x2+ax+b(x∈R)中a,b∈R,若对于任意的a∈[-3,3],关于x的不等式f(x)>1在[-1,1]上恒成立,则b的取值范围是( )
| A.(-∞,2) | B.(-∞,3) | C.(2,+∞) | D.(3,+∞) |
函数f(x)=x2+ax+b的对称轴为x=-
,a∈[-3,3],
①当-
≤-
<-1时,即2<a≤3时,函数f(x)在[-1,1]上是增函数,
函数f(x)在[-1,1]上的最小值为f(-1)=1-a+b>1,此时b>a,故b>3.
②当-1≤-
≤1时,即-2≤a≤2时,函数f(x)在[-1,1]上的最小值为f(-
)=b-
>1,
可得 b>2.
③当1<-
≤
时,即-3≤a<-2时,函数f(x)在[-1,1]上是减函数,
函数f(x)在[-1,1]上的最小值为f(1)=1+a+b>1,此时b>-a,故b>3,
综上可得,b>3,
故选D.
| a |
| 2 |
①当-
| 3 |
| 2 |
| a |
| 2 |
函数f(x)在[-1,1]上的最小值为f(-1)=1-a+b>1,此时b>a,故b>3.
②当-1≤-
| a |
| 2 |
| a |
| 2 |
| a2 |
| 4 |
可得 b>2.
③当1<-
| a |
| 2 |
| 3 |
| 2 |
函数f(x)在[-1,1]上的最小值为f(1)=1+a+b>1,此时b>-a,故b>3,
综上可得,b>3,
故选D.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
 ,则下列不等式成立的是( )
,则下列不等式成立的是( )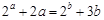 ,则
,则

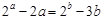 ,则
,则