题目内容
设函数f(x)=ax3+bx2+cx+d是奇函数,且当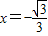 时,f(x)取得极小值
时,f(x)取得极小值 .
.(1)求函数f(x)的解析式;
(2)求使得方程
 仅有整数根的所有正实数n的值;
仅有整数根的所有正实数n的值;(3)设g(x)=|f(x)+(3t-1)x|,(x∈[-1,1]),求g(x)的最大值F(t).
【答案】分析:(1)由f(x)为奇函数,知b=d=0,由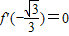 及
及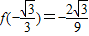 ,知a=-1,c=1,由此能求出f(x).
,知a=-1,c=1,由此能求出f(x).
(2)由方程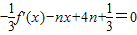 ,知x2-nx+4n=0,由方程仅有整数解,知n为整数,由x2=n(x-4)及n>0知,x-4>0,由此能求出n.
,知x2-nx+4n=0,由方程仅有整数解,知n为整数,由x2=n(x-4)及n>0知,x-4>0,由此能求出n.
(3)由g(x)=|x3-3tx|,x∈[-1,1]是偶函数,知只要求出g(x)在[0,1]上的最大值即可.构造函数h(x)=x3-3tx,利用导数性质能求出g(x)的最大值F(t).
解答:解:(1)∵f(x)为奇函数,∴b=d=0,…(2分)
又由 及
及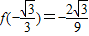 ,得a=-1,c=1,
,得a=-1,c=1,
∴f(x)=-x3+x.…(4分)
当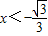 时,f'(x)<0,
时,f'(x)<0,
当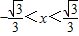 时f'(x)>0,
时f'(x)>0,
∴f(x)在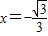 时取得极小值,
时取得极小值,
∴f(x)=-x3+x为所求.…(5分)
(2)方程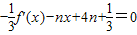 ,
,
化简得:x2-nx+4n=0,
因为方程仅有整数解,故n为整数,
又由x2=n(x-4)及n>0知,x-4>0.…(7分)
又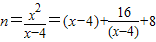 ,
,
故x-4为16的正约数,…(9分)
所以x-4=1,2,4,8,16,进而得到n=16,18,25.…(10分)
(3)因为g(x)=|x3-3tx|,x∈[-1,1]是偶函数,
所以只要求出g(x)在[0,1]上的最大值即可.
记h(x)=x3-3tx,∵h'(x)=3x2-3t=3(x2-t),
①t≤0时,h'(x)≥0,h(x)在[0,1]上单调增且h(x)≥h(0)=0.
∴g(x)=h(x),故F(t)=h(1)=1-3t.…(12分)
②t>0时,由h'(x)=0得,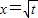 ,和
,和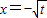 ,
,
i.当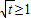 即t≥1时,h(x)在[0,1]上单调减,
即t≥1时,h(x)在[0,1]上单调减,
∴h(x)≤h(0)=0,故g(x)=-h(x),F(t)=-h(1)=3t-1.…(14分)
ii.当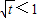 即0<t<1时,h(x)在
即0<t<1时,h(x)在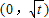 单调减,
单调减,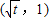 单调增,
单调增,
(Ⅰ)当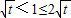 ,即
,即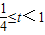 时,
时,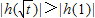 ,∴
,∴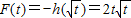 ,
,
(Ⅱ)当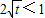 ,即
,即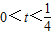 时,
时,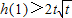 ,∴F(t)=h(1)=1-3t,
,∴F(t)=h(1)=1-3t,
综上可知,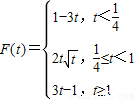 .…(16分)
.…(16分)
点评:本题考查函数的解析式的求法,考查所有正实数值的求法,考查函数的最大值的求法,解题时时要认真审题,注意等价转化思想的合理运用.
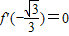 及
及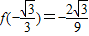 ,知a=-1,c=1,由此能求出f(x).
,知a=-1,c=1,由此能求出f(x).(2)由方程
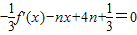 ,知x2-nx+4n=0,由方程仅有整数解,知n为整数,由x2=n(x-4)及n>0知,x-4>0,由此能求出n.
,知x2-nx+4n=0,由方程仅有整数解,知n为整数,由x2=n(x-4)及n>0知,x-4>0,由此能求出n.(3)由g(x)=|x3-3tx|,x∈[-1,1]是偶函数,知只要求出g(x)在[0,1]上的最大值即可.构造函数h(x)=x3-3tx,利用导数性质能求出g(x)的最大值F(t).
解答:解:(1)∵f(x)为奇函数,∴b=d=0,…(2分)
又由
 及
及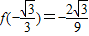 ,得a=-1,c=1,
,得a=-1,c=1,∴f(x)=-x3+x.…(4分)
当
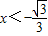 时,f'(x)<0,
时,f'(x)<0,当
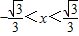 时f'(x)>0,
时f'(x)>0,∴f(x)在
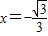 时取得极小值,
时取得极小值,∴f(x)=-x3+x为所求.…(5分)
(2)方程
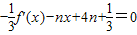 ,
,化简得:x2-nx+4n=0,
因为方程仅有整数解,故n为整数,
又由x2=n(x-4)及n>0知,x-4>0.…(7分)
又
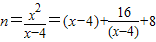 ,
,故x-4为16的正约数,…(9分)
所以x-4=1,2,4,8,16,进而得到n=16,18,25.…(10分)
(3)因为g(x)=|x3-3tx|,x∈[-1,1]是偶函数,
所以只要求出g(x)在[0,1]上的最大值即可.
记h(x)=x3-3tx,∵h'(x)=3x2-3t=3(x2-t),
①t≤0时,h'(x)≥0,h(x)在[0,1]上单调增且h(x)≥h(0)=0.
∴g(x)=h(x),故F(t)=h(1)=1-3t.…(12分)
②t>0时,由h'(x)=0得,
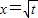 ,和
,和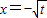 ,
,i.当
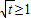 即t≥1时,h(x)在[0,1]上单调减,
即t≥1时,h(x)在[0,1]上单调减,∴h(x)≤h(0)=0,故g(x)=-h(x),F(t)=-h(1)=3t-1.…(14分)
ii.当
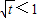 即0<t<1时,h(x)在
即0<t<1时,h(x)在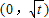 单调减,
单调减,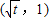 单调增,
单调增,(Ⅰ)当
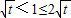 ,即
,即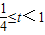 时,
时,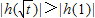 ,∴
,∴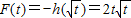 ,
,(Ⅱ)当
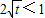 ,即
,即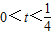 时,
时,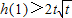 ,∴F(t)=h(1)=1-3t,
,∴F(t)=h(1)=1-3t,综上可知,
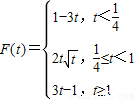 .…(16分)
.…(16分)点评:本题考查函数的解析式的求法,考查所有正实数值的求法,考查函数的最大值的求法,解题时时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 设函数f(x)=(a
设函数f(x)=(a| x |
| 1 | ||
|
| ∫ | 2π π |
A、-
| ||
| B、-160 | ||
| C、160 | ||
| D、20 |