题目内容
(本小题满分16分)
已知数列 前
前 项和
项和 .数列
.数列 满足
满足
 ,数列
,数列 满足
满足 。(1)求数列
。(1)求数列 和数列
和数列 的通项公式;(2)求数列
的通项公式;(2)求数列 的前
的前 项和
项和 ;(3)若
;(3)若 对一切正整数
对一切正整数 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
(1)数列 的通项公式为
的通项公式为 ;
;
(2) 。(3)
。(3)
解析试题分析:(1)由已知和得,当 时,
时,
又 ,符合上式。故数列
,符合上式。故数列 的通项公式
的通项公式 。
。
又∵ ,∴
,∴ ,
,
故数列 的通项公式为
的通项公式为 , …………5分
, …………5分
(2) ,
, ,
,  ,
,
①-②得 

 ,
,
∴  。 …………10分
。 …………10分
(3)∵ ,
,
∴
 ,
,
当 时,
时, ;当
;当 时,
时, ,∴
,∴ 。
。
若 对一切正整数
对一切正整数 恒成立,则
恒成立,则 即可,
即可,
∴ …………16分
…………16分
考点:本题考查数列通项公式的求法,前n项和的求法;数列与不等式的综合应用。
点评:该题考查求数列的通项与数列求和.若已知sn求通项公式an,分n=1与n≥2两种情况讨论,当n=1符合n≥2时的结果,通项公式要合为一个。等差数列与等比数列的乘积构成的数列求前n项和用错位相减法,此题综合性强.

练习册系列答案
相关题目
下列命题为真命题的是( )
A.若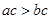 ,则 ,则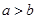 |
B.若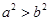 ,则 ,则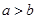 |
C.若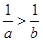 ,则 ,则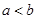 |
D.若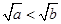 ,则 ,则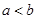 |
 满足
满足 ,数列
,数列 满足
满足 ,
, 满足
满足 .
. ,证明数列
,证明数列 ,证明数列
,证明数列 的前
的前 项和
项和 满足
满足 。
。 的前n项和,求Tn.
的前n项和,求Tn. 的前
的前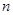 项和
项和 。(1)求数列
。(1)求数列 ,且数列
,且数列 的前
的前 。若
。若 ,求
,求 中,
中, .
. 的顺序,使它成为等比数列
的顺序,使它成为等比数列 的前三项,求
的前三项,求 项和.
项和.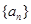 ,前
,前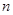 项和为
项和为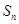 .且满足
.且满足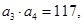
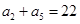 .
.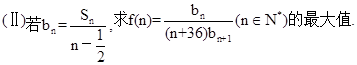
 的前
的前 项和为
项和为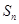 ,且满足
,且满足 (
( 满足
满足 ,且
,且 ,求数列
,求数列