题目内容
(本小题满分12分)
数列{an}的前n项和记为Sn,已知a1=1,an+1=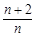 Sn(n=1,2,3…).
Sn(n=1,2,3…).
求证:数列{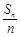 }是等比数列.
}是等比数列.
{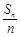 }是以2为公比的等比数列.
}是以2为公比的等比数列.
解析试题分析:求证数列是否为等比数列,主要是看该数列的相邻两项的比值是否为定值,注意从第二项起来证明即可。证明:∵an+1=Sn+1-Sn,an+1=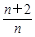 Sn, 3分
Sn, 3分
∴(n+2)Sn=n(Sn+1-Sn),整理得nSn+1=2(n+1) Sn, 6分
所以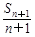 =
=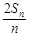 .又
.又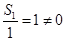 10分
10分
故{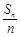 }是以2为公比的等比数列. 12分
}是以2为公比的等比数列. 12分
考点:等比数列
点评:考查了等比数列的定义的运用,注意根据相邻项的比值为定值来得到结论,属于基础题。

练习册系列答案
相关题目
等差数列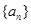 、
、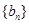 的前n项和分别为
的前n项和分别为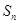 和
和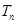 ,若
,若 ,则
,则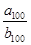 = ( )
= ( )
| A.1 | B.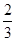 | C.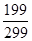 | D.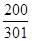 |
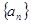 中,
中,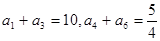 ,求其第4项及前5项和.
,求其第4项及前5项和.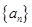 的前
的前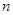 项和为
项和为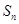 .已知
.已知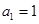 ,
,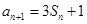 ,
,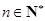 .
.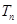 为数列
为数列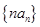 的前
的前 ,已知
,已知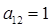 ,
,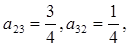 又设第一行数列的公差为
又设第一行数列的公差为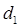 .
.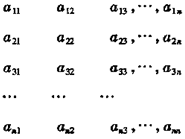
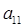 ,
,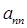 的表达式,并求
的表达式,并求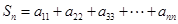 的值.
的值.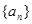 中,
中,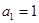 ,且
,且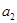 是
是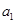 和
和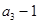 的等差中项.
的等差中项. 满足
满足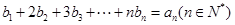 ,求
,求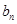 .
. 满足
满足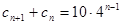 ,
, ,数列
,数列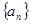 满足
满足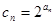
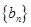 满足
满足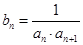 ,
,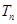 为数列
为数列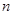 项和.求
项和.求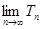 ;(5分)
;(5分)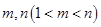 ,使得
,使得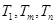 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有 的值;若不存在,请说明理由.(6分)
的值;若不存在,请说明理由.(6分)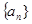 的前n项和
的前n项和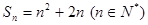 .
.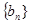 是等比数列,公比为
是等比数列,公比为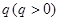 ,且满足
,且满足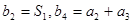 ,求数列
,求数列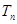 .
.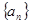 是公差不为零的等差数列,
是公差不为零的等差数列,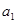 =1,且
=1,且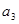 ,
,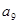 成等比数列.
成等比数列.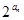 }的前n项和
}的前n项和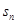 .
.