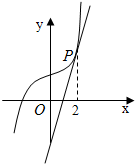题目内容
f(x)=![]() ax3+bx2+cx+d,其中a、b、c、是以d为公差的等差数列,且a>0,d>0,设x0为f(x)的极小值点。在[1-
ax3+bx2+cx+d,其中a、b、c、是以d为公差的等差数列,且a>0,d>0,设x0为f(x)的极小值点。在[1-![]() ,0]上,f /(x)在x1处取最大值,在x2处取最小值,记点A(x0 ,f(x0)),B(x1 ,f/(x1)),C(x2 ,f/(x2))。
,0]上,f /(x)在x1处取最大值,在x2处取最小值,记点A(x0 ,f(x0)),B(x1 ,f/(x1)),C(x2 ,f/(x2))。
(1)求x0的值;
(2)若△ABC有一条边平行于x轴,且面积为2+![]() ,求a、d的值。
,求a、d的值。
解:(1)∵2b=a+c
f/(x)=ax2+2bx+c= ax2+(a+c)x+c=a(x+1)(x+![]() )
)
∵a>0,d>0,∴![]() >1,
>1,
令f/(x)=0,得:x1=-![]() ,x2=-1,x1<x2,
,x2=-1,x1<x2,
列表可知,x1为极小值点,x2为极大值点;∴x0=-1;
(2)f/(x)的图象是开口向上,对称轴为x=-![]() 的抛物线,-
的抛物线,-![]() <-1,
<-1,
由f/(x)在[1-![]() ,0]上的图象可知:最大值为f/(0)=c,即x1=0,
,0]上的图象可知:最大值为f/(0)=c,即x1=0,
f/(x)在[1-![]() ,0]上的最小值为f/(-
,0]上的最小值为f/(-![]() )=-
)=-![]() ,即x2=-
,即x2=-![]() ,
,
∴A(-1,-![]() ),B(0,c),C(-
),B(0,c),C(-![]() ,-
,-![]() )
)
∵△ABC的一边平行于x轴,∴AC平行于x轴,
∴-![]() =-
=-![]() ∴a=
∴a=![]() d,
d,
b=(![]() +1)d,c=(
+1)d,c=(![]() +2)d,代入
+2)d,代入
S△=![]() |(
|(![]() -1)(C+
-1)(C+![]() )|=2+
)|=2+![]() 得:
得:
∴d=3,a=3![]() 。
。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知函数f(x)=ax3+b,其图象在点P处的切线为l:y=4x-4,点P的横坐标为2(如图).求直线l、直线x=0、直线y=0以及f(x)的图象在第一象限所围成区域的面积.
已知函数f(x)=ax3+b,其图象在点P处的切线为l:y=4x-4,点P的横坐标为2(如图).求直线l、直线x=0、直线y=0以及f(x)的图象在第一象限所围成区域的面积. 已知函数f(x)=ax3+b,其图象在点P处的切线为l:y=4x-4,点P的横坐标为2(如图).求直线l、直线x=0、直线y=0以及f(x)的图象在第一象限所围成区域的面积.
已知函数f(x)=ax3+b,其图象在点P处的切线为l:y=4x-4,点P的横坐标为2(如图).求直线l、直线x=0、直线y=0以及f(x)的图象在第一象限所围成区域的面积.