题目内容
9.已知函数f(x)=sin(ωx+$\frac{π}{2}$)(ω>0),f($\frac{π}{6}$)=f($\frac{π}{3}$),且f(x)在区间[$\frac{π}{6}$,$\frac{π}{3}$]上有最小值,无最大值,则ω的值为4.分析 由题意可得f(x)的图象关于直线x=$\frac{π}{4}$对称,f($\frac{π}{4}$)=sin($\frac{π}{4}$ω+$\frac{π}{2}$)=-1,即即ω=8k-4;再结合$\frac{π}{3}$-$\frac{π}{4}$<$\frac{T}{2}$=$\frac{π}{ω}$,求得ω的值.
解答 解:由f($\frac{π}{6}$)=f($\frac{π}{3}$),可得f(x)的图象关于直线x=$\frac{\frac{π}{6}+\frac{π}{3}}{2}$=$\frac{π}{4}$对称.
再根据f(x)在区间[$\frac{π}{6}$,$\frac{π}{3}$]上有最小值,可得f($\frac{π}{4}$)=sin($\frac{π}{4}$ω+$\frac{π}{2}$)=-1,
∴$\frac{π}{4}$ω+$\frac{π}{2}$=2kπ-$\frac{π}{2}$,k∈z,即ω=8k-4,k∈z.
再根据f(x)在区间[$\frac{π}{6}$,$\frac{π}{3}$]上无最大值,$\frac{π}{3}$-$\frac{π}{4}$<$\frac{T}{2}$=$\frac{π}{ω}$,求得ω<12.
综合可得ω=4,
故答案为:4.
点评 本题主要考查正弦函数的图象特征,正弦函数的图象的对称性、定义域和值域,属于基础题.

练习册系列答案
相关题目
17.复数z=|$\sqrt{3}$-i|+i(i为虚数单位),则复数z的共轭复数为( )
| A. | 2-i | B. | 2+i | C. | 4-i | D. | 4+i |
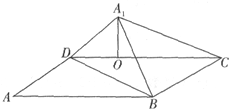 如图,将矩形ABCD沿对角线BD把△ABD折起,使A点移到A1点,且A1在平面BCD上的射影O恰好在CD上.
如图,将矩形ABCD沿对角线BD把△ABD折起,使A点移到A1点,且A1在平面BCD上的射影O恰好在CD上.