题目内容
若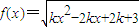 的定义域为R,则实数k的取值范围是 .
的定义域为R,则实数k的取值范围是 .
【答案】分析: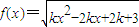 的定义域为R,开偶次方,被开方数为非负,求出k即可.
的定义域为R,开偶次方,被开方数为非负,求出k即可.
解答:解: 的定义域为R,
的定义域为R,
所以kx2-2kx+2k+3≥0,恒成立,
当k=0时,上式显然成立;
当k>0时,只需:4k2-4k(2k+3)≤0解得k>0
综上:k≥0
故答案为:[0,+∞)
点评:本题考查函数的定义域及其求法,函数恒成立问题,考查计算能力,是基础题.
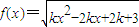 的定义域为R,开偶次方,被开方数为非负,求出k即可.
的定义域为R,开偶次方,被开方数为非负,求出k即可.解答:解:
 的定义域为R,
的定义域为R,所以kx2-2kx+2k+3≥0,恒成立,
当k=0时,上式显然成立;
当k>0时,只需:4k2-4k(2k+3)≤0解得k>0
综上:k≥0
故答案为:[0,+∞)
点评:本题考查函数的定义域及其求法,函数恒成立问题,考查计算能力,是基础题.

练习册系列答案
相关题目
f(x)的定义域为R,且f(x)=
,若方程f(x)=x+a有两不同实根,则a的取值范围为( )
|
| A、(-∞,1) |
| B、(-∞,1] |
| C、(0,1) |
| D、(-∞,+∞) |
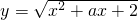 在区间(-∞,1]上是减函数,则实数a∈[-3,-2];
在区间(-∞,1]上是减函数,则实数a∈[-3,-2]; 对称.
对称.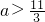 ;
;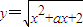 在区间(-∞,1]上是减函数,则实数a∈[-3,-2];
在区间(-∞,1]上是减函数,则实数a∈[-3,-2];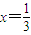 对称.
对称.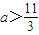 ;
;