题目内容
函数f(x)的定义域为R,且f(x)=
,若方程f(x)=x+a有两个不同实根,则a的取值范围是
|
a<1
a<1
.分析:由已知中函数的解析式,我们易分析出函数的图象在Y轴右侧呈周期性变化,结合函数在x≤0时的解析式,我们可以画出函数的像,根据图象易分析出满足条件的a的取值范围.
解答:解:①当x≤0时,f(x)=2-x-1,
②当0<x≤1时,-1<x-1≤0,f(x)=f(x-1)=2-(x-1)-1.
当1<x≤2时,-1<x-2≤0,f(x)=f(x-1)=f(x-2)=2-(x-2)-1.
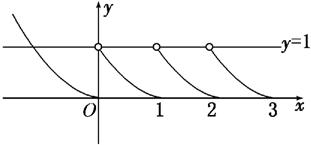
故x>0时,f(x)是周期函数,如图,
欲使方程f(x)=x+a有两解,
即函数f(x)的图象与直线y=x+a有两个不同交点,
所以a<1.
故答案为:a<1.
②当0<x≤1时,-1<x-1≤0,f(x)=f(x-1)=2-(x-1)-1.
当1<x≤2时,-1<x-2≤0,f(x)=f(x-1)=f(x-2)=2-(x-2)-1.
故x>0时,f(x)是周期函数,如图,
欲使方程f(x)=x+a有两解,
即函数f(x)的图象与直线y=x+a有两个不同交点,
所以a<1.

故答案为:a<1.
点评:本题考查的知识点是函数的图象与图象变化,其中根据函数的解析式,分析函数的性质,并画出函数的图象是解答本题的关键.

练习册系列答案
相关题目
若函数f(x)的定义域为[-1,2],则函数
的定义域为( )
| f(x+2) |
| x |
| A、[-1,0)∪(0,2] |
| B、[-3,0) |
| C、[1,4] |
| D、(0,2] |