题目内容
(本题满分14分)已知函数 的图象在点
的图象在点 处的切线的斜率为
处的切线的斜率为 ,且在
,且在 处取得极小值。
处取得极小值。
(1)求 的解析式;
的解析式;
(2)已知函数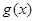 定义域为实数集
定义域为实数集 ,若存在区间
,若存在区间 ,使得
,使得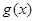 在
在 的值域也是
的值域也是 ,称区间
,称区间 为函数
为函数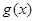 的“保值区间”.
的“保值区间”.
①当 时,请写出函数
时,请写出函数 的一个“保值区间”(不必证明);
的一个“保值区间”(不必证明);
②当 时,问
时,问 是否存在“保值区间”?若存在,写出一个“保值区间”并给予证明;若不存在,请说明理由.
是否存在“保值区间”?若存在,写出一个“保值区间”并给予证明;若不存在,请说明理由.
解:(1)∵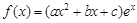 ,
,
∴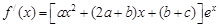 …… 1 分
…… 1 分
由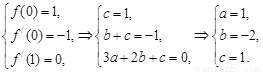 …… 4 分
…… 4 分
∴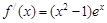 , 令
, 令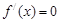 ,解得
,解得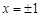 ,
,
当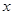 变化时,
变化时,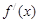 ,
,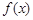 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
1 |
|
|
|
|
0 |
|
0 |
+ |
|
|
↗ |
极大值 |
↘ |
极小值 |
↗ |
∴当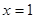 时,
时,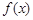 取得极小值。
取得极小值。
所以,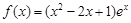 。
…… 5 分
。
…… 5 分
(2) ① 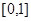 …… 7 分
…… 7 分
②由(1)得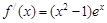 ,
,
假设当x>1时,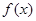 存在“保值区间”:[m,n](n>m>1)。
存在“保值区间”:[m,n](n>m>1)。
因为当x>1时,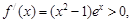 所以
所以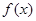 在区间
在区间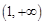 是增函数,
是增函数,
依题意, 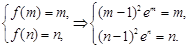
于是问题转化为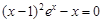 有两个大于1的根。
…… 9 分
有两个大于1的根。
…… 9 分
现在考察函数
则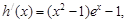 令
令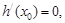
又∵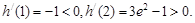
∴1<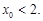
当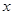 变化时,
变化时,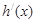 ,
,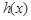 的变化情况如下表:
的变化情况如下表:
|
|
(1, |
|
|
|
|
- |
0 |
+ |
|
|
单调递减 |
极小值 |
单调递增 |
所以,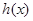 在在(1,
在在(1,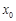 ) 上单调递减, 在
) 上单调递减, 在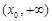 上单调递增。 …… 12 分
上单调递增。 …… 12 分
于是,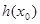
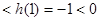 ,
,
又因为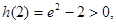
所以,当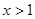 时,
时,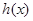 的图象与
的图象与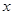 轴只有一个交点,
…… 13 分
轴只有一个交点,
…… 13 分
即方程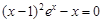 有且只有一个大于1的根,与假设矛盾。
有且只有一个大于1的根,与假设矛盾。
故当x>1时,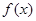 不存在“保值区间”。
…… 14 分
不存在“保值区间”。
…… 14 分
(2)解法2:由(1)得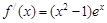 ,
,
② 假设当x>1时,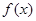 存在“保值区间”:[m,n](n>m>1)。
存在“保值区间”:[m,n](n>m>1)。
因为当x>1时,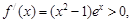 所以
所以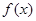 在区间
在区间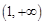 是增函数,
是增函数,
依题意, 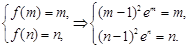
于是问题转化为方程 ,即
,即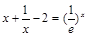 有两个大于1的根。…… 9 分
有两个大于1的根。…… 9 分
考察函数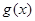 =
=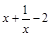 (
(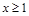 ),与函数
),与函数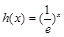 (
(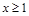 ).
).
当x>1时,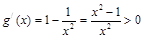 ,
,
所以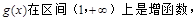
而函数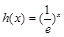 在区间
在区间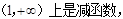 …… 12 分
…… 12 分
又因为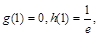 所以
所以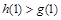 ,
,
因此函数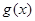 =
=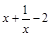 (
(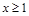 )的图象与函数
)的图象与函数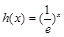 (
(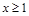 )的图象只有一个交点。
)的图象只有一个交点。
…… 13分
即方程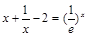 有且只有一大于1的根,与假设矛盾。
有且只有一大于1的根,与假设矛盾。
故当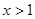 时,
时,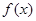 不存在“保值区间”
不存在“保值区间”
【解析】略

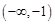
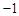
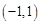


 ,求x的值;
,求x的值; 对于
对于 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.  :
: 的离心率为
的离心率为 ,过坐标原点
,过坐标原点 且斜率为
且斜率为 的直线
的直线 与
与 、
、 ,
, .
. 、
、 的值;
的值; 与椭圆
与椭圆 的取值范围.
的取值范围. ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图). ,
,
