题目内容
16.已知复数z1=1+2i,z2=2-2i,i为虚数单位.(1)若复数az1+z2在复平面内对应的点在第三象限,求实数a的取值范围;
(2)若z=$\frac{{z}_{1}+{z}_{2}}{{z}_{1}-{z}_{2}}$,求z的共轭复数$\overline{z}$.
分析 (1)根据复数的几何意义建立不等式关系即可;
(2)根据复数的运算法则化简复数z=$\frac{{z}_{1}+{z}_{2}}{{z}_{1}-{z}_{2}}$,即可求z的共轭复数$\overline{z}$.
解答 解:(1)az1+z2=a+2ai+2-2i=(a+2)+2(a-1)i,
若复数在复平面内对应的点在第三象限,
则$\left\{\begin{array}{l}{a+2<0}\\{2(a-1)<0}\end{array}\right.$,即$\left\{\begin{array}{l}{a<-2}\\{a<1}\end{array}\right.$,
解得a<-2,即实数a的取值范围是(-∞,-2);
(2)z=$\frac{{z}_{1}+{z}_{2}}{{z}_{1}-{z}_{2}}$=$\frac{1+2i+2-2i}{1+2i-2+2i}$=$\frac{3}{-1+4i}$=$\frac{3(-1-4i)}{(-1+4i)(-1-4i)}$=$\frac{-3-12i}{17}$=$-\frac{3}{17}$-$\frac{12}{17}$i,
则z的共轭复数$\overline{z}$=$-\frac{3}{17}$+$\frac{12}{17}$i.
点评 本题主要考查复数的几何意义以及复数的基本运算,考查学生的运算能力.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
6.空间向量不可以做的运算是( )
| A. | 加法 | B. | 减法 | C. | 数量积 | D. | 除法 |
 在平面直角坐标系xOy中,点A(-1,-2)、B(2,3)、C(-2,-1).
在平面直角坐标系xOy中,点A(-1,-2)、B(2,3)、C(-2,-1). 函数f(x)=ax+b的图象如图,其中a,b为常数,给出下列四种说法:①a>1,b>0;②0<a<1,b<0;③a>1,b>-1;④a>1,b<-1.则其中所有正确说法的序号是④.
函数f(x)=ax+b的图象如图,其中a,b为常数,给出下列四种说法:①a>1,b>0;②0<a<1,b<0;③a>1,b>-1;④a>1,b<-1.则其中所有正确说法的序号是④.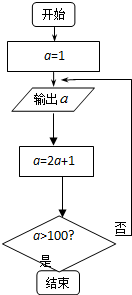 按照如图所示的框图操作,
按照如图所示的框图操作,