题目内容
【题目】二次函数![]() 图像与
图像与![]() 轴交于
轴交于![]() ,
,![]() 两点,交直线
两点,交直线![]() 于
于![]() ,
,![]() 两点,经过三点
两点,经过三点![]() ,
,![]() ,
,![]() 作圆
作圆![]() .
.
(1)求证:当![]() 变化时,圆
变化时,圆![]() 的圆心在一条定直线上;
的圆心在一条定直线上;
(2)求证:圆![]() 经过除原点外的一个定点.
经过除原点外的一个定点.
【答案】(1)证明见解析(2)证明见解析
【解析】
(1)联立![]() ,
,![]() 求得点
求得点![]() ,联立
,联立![]() 与
与![]() 求得点
求得点![]() ,设圆C的方程为
,设圆C的方程为![]() ,根据
,根据![]() 点到圆心距离相等求得圆心坐标x0与y0的联系,消参即可求得定直线
点到圆心距离相等求得圆心坐标x0与y0的联系,消参即可求得定直线
(2)由(1)知,设圆C过定点(m,n),则m2+n2+bm+(b﹣2)n=0,整理成关于b的一次函数形式,根据恒成立问题联立方程求解即可
解:(1)在方程![]() 中.令
中.令![]() ,易得
,易得![]()
设圆C的方程为![]()
则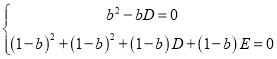
![]() ,
,
故经过三点O,A,B的圆C的方程为x2+y2+bx+(b﹣2)y=0,
设圆C的圆心坐标为(x0,y0),
则![]() ,∴y0=x0+1,
,∴y0=x0+1,
这说明当b变化时,(1)中的圆C的圆心在定直线y=x+1上
(2)设圆C过定点(m,n),则m2+n2+bm+(b﹣2)n=0,整理得(m+n)b+m2+n2﹣2n=0,
它对任意b≠0恒成立,∴![]()
故当b变化时,(1)中的圆C经过除原点外的一个定点坐标为(﹣1,1).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
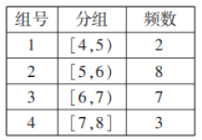
小学生10分钟应用题系列答案【题目】在某校举行的航天知识竞赛中,参与竞赛文科生与理科生人数之比为![]() ,且成绩分布在
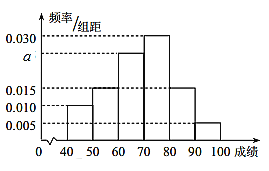
,且成绩分布在![]() ,分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图如图所示.
,分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图如图所示.
文科生 | 理科生 | 合计 | |
获奖 | 5 | ||
不获奖 | |||
合计 | 200 |
参考公式: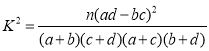 (其中
(其中![]() 为样本容量)
为样本容量)
随机变量![]() 的概率分布:
的概率分布:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.001 | |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)求![]() 的值;
的值;
(2)填写上方的![]() 列联表,并判断能否有超过
列联表,并判断能否有超过![]() 的把握认为“获奖与学生的文、理科有关”?
的把握认为“获奖与学生的文、理科有关”?
【题目】汽车尾气中含有一氧化碳![]() ,碳氢化合物
,碳氢化合物![]() 等污染物,是环境污染的主要因素之一,汽车在使用若干年之后排放的尾气之中的污染物会出现递增的现象,所以国家根据机动车使用和安全技术、排放检验状况,对达到报废标准的机动车实施强制报废,某环境组织为了解公众对机动车强制报废标准的了解情况,随机调查了
等污染物,是环境污染的主要因素之一,汽车在使用若干年之后排放的尾气之中的污染物会出现递增的现象,所以国家根据机动车使用和安全技术、排放检验状况,对达到报废标准的机动车实施强制报废,某环境组织为了解公众对机动车强制报废标准的了解情况,随机调查了![]() 人,所得数据制成如下列联表:
人,所得数据制成如下列联表:

(1)若从这![]() 人中任选
人中任选![]() 人,选到了解强制报废标准的人的概率为
人,选到了解强制报废标准的人的概率为![]() ,问是否在犯错的概率不超过5﹪的前提下认为“机动车强制报废标准是否了解与性别有关”?
,问是否在犯错的概率不超过5﹪的前提下认为“机动车强制报废标准是否了解与性别有关”?
(2)该环保组织从相关部门获得某型号汽车的使用年限与排放的尾气中![]() 浓度的数据,并制成如图所示的折线图,若该型号汽车的使用年限不超过
浓度的数据,并制成如图所示的折线图,若该型号汽车的使用年限不超过![]() 年,可近似认为排放的尾气中
年,可近似认为排放的尾气中![]() 浓度
浓度![]() ﹪与使用年限
﹪与使用年限![]() 线性相关,确定
线性相关,确定![]() 与
与![]() 的回归方程,并预测该型号的汽车使用
的回归方程,并预测该型号的汽车使用![]() 年排放尾气中的
年排放尾气中的![]() 浓度是使用
浓度是使用![]() 年的多少倍.
年的多少倍.

附:![]() ,
,
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |