题目内容
一个样本容量为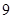 的样本数据,它们组成一个公差不为
的样本数据,它们组成一个公差不为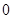 的等差数列
的等差数列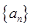 ,若
,若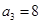 ,且
,且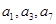 成等比数列,则此样本的中位数是
成等比数列,则此样本的中位数是
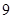 的样本数据,它们组成一个公差不为
的样本数据,它们组成一个公差不为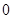 的等差数列
的等差数列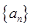 ,若
,若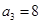 ,且
,且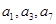 成等比数列,则此样本的中位数是
成等比数列,则此样本的中位数是A.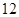 | B.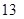 | C.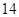 | D.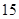 |
A
分析:由题设条件,一个样本容量为8的样本数据,它们组成一个公差不为0的等差数列{an},若a3=8,且a1,a3,a7成等比数列,设出公差为d,用公差与与a3=8表示出a1,a7再由等比数列的性质建立方程求出公差,即可得到样本数据,再由公式求出样本的平均数和中位数
解答:解:设公差为d,由a3=8,且a1,a3,a7成等比数列,可得64=(8-2d)(8+4d)=64+16d-8d2,即,0=16d-8d2,又公差不为0,解得d=2
此数列的各项分别为4,6,8,10,12,14,16,18,20,
故样本的中位数是12,
故答案为A
解答:解:设公差为d,由a3=8,且a1,a3,a7成等比数列,可得64=(8-2d)(8+4d)=64+16d-8d2,即,0=16d-8d2,又公差不为0,解得d=2
此数列的各项分别为4,6,8,10,12,14,16,18,20,
故样本的中位数是12,
故答案为A

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
 秒,黄灯的时间为
秒,黄灯的时间为 秒,绿灯的时间为
秒,绿灯的时间为 秒,当你到达路口时看见下列三种情况的概率各是多少?
秒,当你到达路口时看见下列三种情况的概率各是多少? 与
与 之间的一组数据如下表,根据表中提供的数据,求出
之间的一组数据如下表,根据表中提供的数据,求出 , 那么
, 那么  的值为( )
的值为( )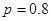 ,则输出的
,则输出的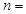 ______;
______;  ,方差是
,方差是 ,那么另一组数据
,那么另一组数据
 总体标准差的点估计值为 (结果精确到0.01).
总体标准差的点估计值为 (结果精确到0.01).  =_________
=_________
 某段时间内幼崽出生的时间与性别的关系,得到下面的数据表:
某段时间内幼崽出生的时间与性别的关系,得到下面的数据表:


