题目内容
【题目】在三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,设
的中点,设![]() .当
.当![]() 时,
时,![]() ____________.
____________.
【答案】![]()
【解析】
由正弦定理得![]() ,
,![]() ,由此能
,由此能
sinβ![]() ,cosβ
,cosβ![]() ,tanα=sin∠BAC=sin(α+β)得cosα
,tanα=sin∠BAC=sin(α+β)得cosα![]() ,sinα
,sinα![]() ,从而得到cos∠BAC
,从而得到cos∠BAC![]() ,由此利用余弦定理能求出BC.
,由此利用余弦定理能求出BC.
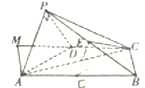
∵在△ABC中,AB=2,AC=4,![]() 是
是![]() 的中点,记∠CAD=α,∠BAD=β,
的中点,记∠CAD=α,∠BAD=β,
∴![]() ,
,![]() ,
,
∴sin![]() ,sin
,sin![]() =
=![]() CDsin∠ADC,
CDsin∠ADC,
∵BD=CD,sin∠ADB=sin∠ADC,
∴sinα:sinβ=![]() :
:![]() CDsin∠ADC
CDsin∠ADC![]() 2:1.
2:1.
即得sinβ![]() ,cosβ
,cosβ![]() ,
,
∴tanα=sin(α+β)=sinαcosβ+cosαsinβ
=sinα![]() ,
,
∴![]() ,
,
∴cos2α+cosα![]() 2,解得cosα
2,解得cosα![]() ,或cosα
,或cosα![]() (舍),sinα
(舍),sinα![]() ,
,
∴sin∠BAC ,cos∠BAC
,cos∠BAC![]() ,
,
∴BC![]() .
.
故答案为![]() .
.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
【题目】为普及学生安全逃生知识与安全防护能力,某学校高一年级举办了安全知识与安全逃生能力竞赛,该竞赛分为预赛和决赛两个阶段,预赛为笔试,决赛为技能比赛,现将所有参赛选手参加笔试的成绩(得分均为整数,满分为![]() 分)进行统计,制成如下频率分布表.
分)进行统计,制成如下频率分布表.
分数(分数段) | 频数(人数) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
(1)求表中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)按规定,预赛成绩不低于![]() 分的选手参加决赛.已知高一(2)班有甲、乙两名同学取得决赛资格,记高一(2)班在决赛中进入前三名的人数为
分的选手参加决赛.已知高一(2)班有甲、乙两名同学取得决赛资格,记高一(2)班在决赛中进入前三名的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.