题目内容
已知椭圆具有性质:若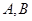 是椭圆
是椭圆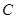 :
: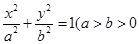 且
且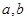 为常数
为常数 上关于原点对称的两点,点
上关于原点对称的两点,点 是椭圆上的任意一点,若直线
是椭圆上的任意一点,若直线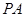 和
和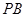 的斜率都存在,并分别记为
的斜率都存在,并分别记为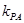 ,
,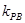 ,那么
,那么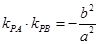 .类比双曲线
.类比双曲线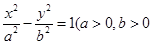 且
且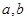 为常数
为常数 中,若
中,若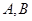 是双曲线
是双曲线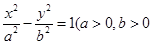 且
且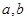 为常数
为常数 上关于原点对称的两点,点
上关于原点对称的两点,点 是双曲线上的任意一点,若直线
是双曲线上的任意一点,若直线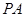 和
和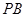 的斜率都存在,并分别记为
的斜率都存在,并分别记为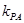 ,
,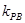 ,那么 .
,那么 .
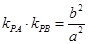
解析试题分析:椭圆两直线斜率乘积为负值,双曲线两直线斜率乘积为正值,由类比推理知: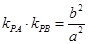 .
.
考点:推理与证明.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
在平面上,若两个正三角形的边长比为1:2.则它们的面积之比为1:4.类似地,在空间中,若两个正四面体的棱长比为1:2,则它们的体积比为( )
| A.1:2 | B.1:4 | C.1:6 | D.1:8 |
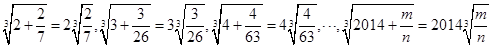 ,则
,则 .
. 表示不超过
表示不超过 的最大整数,如
的最大整数,如 .我们发现:
.我们发现: ;
; ;
; ;
; 的式子表示)
的式子表示)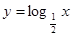 在
在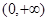 上是减函数”恢复成完全的三段论,其中大前提是 .
上是减函数”恢复成完全的三段论,其中大前提是 .  .
. 中,
中, ,以
,以 为直径的半圆分别交
为直径的半圆分别交 于点
于点 ,若
,若 ,则
,则



 ,
, (其中
(其中 ), 则
), 则 ,
, ,根据上面的结论,可以提出猜想: z1·z2·z3= .
,根据上面的结论,可以提出猜想: z1·z2·z3= .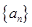 的前
的前 项和为
项和为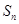 .若数列
.若数列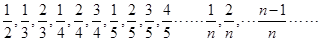 则
则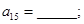 若存在正整数
若存在正整数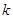 ,使
,使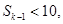
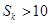 ,则
,则