题目内容
正三棱柱
的各棱长都是2，E，F分别是
的中点，则EF的长是（ ）
| A．2 | B． | C． | D． |
C
解析试题分析：取A1B1的中点M，连接EM，MF，则EM垂直底面A1B1C1，所以在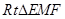
中，
考点：正三棱柱的性质.
点评：利用正三棱柱底面是正三角形，侧棱与底面垂直，可解EF所在的直角三角形EMF求值即可.
练习册系列答案
阳光课堂课时作业系列答案
相关题目
设四面体的六条棱的长分别为1，1，1，1，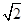
和
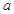，且长为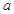的棱与长为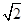的棱异面，则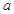的取值范围是
A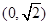． | B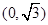． | C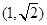． | D． |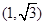
球的表面积与它的内接正方体的表面积之比是（ ）
A． | B． | C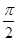． | D． |
如图所示的直观图，其原来平面图形的面积是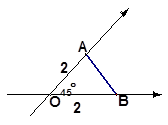
| A．4 |
B．4 |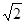
| C．2 |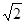
| D．8 |
长方体的一个顶点上三条棱长分别是
，且它的
个顶点都在同一球面上，则这个球的表面积是（ ）
A． | B． | C． | D．都不对 |
已知正方体外接球的体积是
，那么正方体的棱长等于（ ）
A．2 | B． | C． | D． |
