题目内容
9.若实数a,b满足$\frac{1}{a}$+$\frac{2}{b}$=$\sqrt{ab}$,则ab的最小值为( )| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
分析 由$\frac{1}{a}$+$\frac{2}{b}$=$\sqrt{ab}$,可判断a>0,b>0,然后利用基础不等式$\frac{1}{a}+\frac{2}{b}≥2\sqrt{\frac{2}{ab}}$即可求解ab的最小值
解答 解:∵$\frac{1}{a}$+$\frac{2}{b}$=$\sqrt{ab}$,
∴a>0,b>0,
∵$\frac{1}{a}+\frac{2}{b}≥2\sqrt{\frac{2}{ab}}$(当且仅当b=2a时取等号),
∴$\sqrt{ab}≥2\sqrt{\frac{2}{ab}}$,
解可得,ab$≥2\sqrt{2}$,即ab的最小值为2$\sqrt{2}$,
故选:C.
点评 本题主要考查了基本不等式在求解最值中的简单应用,属于基础试题

练习册系列答案
相关题目
1.已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的表面积为( )
| A. | 36π | B. | 64π | C. | 144π | D. | 256π |
19.设命题p:?n∈N,n2>2n,则¬p为( )
| A. | ?n∈N,n2>2n | B. | ?n∈N,n2≤2n | C. | ?n∈N,n2≤2n | D. | ?n∈N,n2=2n |
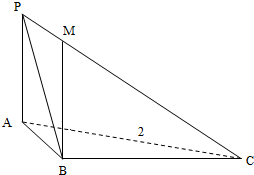 如图,三棱锥P-ABC中,PA⊥平面ABC,PA=1,AB=1,AC=2,∠BAC=60°.
如图,三棱锥P-ABC中,PA⊥平面ABC,PA=1,AB=1,AC=2,∠BAC=60°.