题目内容
【题目】在四棱锥![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() ,
,![]() 的中点.
的中点.
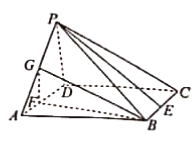
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)证明见解析;(2) ![]()
【解析】
(1)连接![]() ,证明平面
,证明平面![]() 平面
平面![]() ,即可说明
,即可说明![]() 平面
平面![]() ;
;
(2)先计算出![]() ,再利用等体积法
,再利用等体积法![]() ,即可求出点
,即可求出点![]() 到平面
到平面![]() 的距离.
的距离.
(1)证明:连接![]() ,∵在矩形
,∵在矩形![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 中点,
中点,

∴![]() ,
,![]() ,∴四边形
,∴四边形![]() 是平行四边形,∴
是平行四边形,∴![]() .
.
∵![]() 是
是![]() 的中点,∴
的中点,∴![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
∵![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)解:法一:∵![]() 平面
平面![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() .
.
过![]() 在平面
在平面![]() 内,作
内,作![]() ,垂足为
,垂足为![]() ,则
,则![]() .
.
∵![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() 长是点
长是点![]() 到平面
到平面![]() 的距离.
的距离.
在矩形![]() 中,
中,![]() 是
是![]() 中点,
中点,![]() ,
,![]() ,
,![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,∴
,∴![]() ,
,
即点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
法二:设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
在矩形![]() 中,
中,![]() ,
,![]() ,∴
,∴![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() 的面积为
的面积为![]() .
.
∵![]() 的面积为
的面积为![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,即点
,即点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.

练习册系列答案
相关题目
【题目】今年1月至2月由新型冠状病毒引起的肺炎病例陡然增多,为了严控疫情传播,做好重点人群的预防工作,某地区共统计返乡人员![]() 人,其中
人,其中![]() 岁及以上的共有
岁及以上的共有![]() 人.这
人.这![]() 人中确诊的有
人中确诊的有![]() 名,其中
名,其中![]() 岁以下的人占
岁以下的人占![]() .
.
(1)请将下面的列联表补充完整,并判断是否有![]() %的把握认为是否确诊患新冠肺炎与年龄有关;
%的把握认为是否确诊患新冠肺炎与年龄有关;
确诊患新冠肺炎 | 未确诊患新冠肺炎 | 合计 | |
50岁及以上 | 40 | ||
50岁以下 | |||
合计 | 10 | 100 |
(2)为了研究新型冠状病毒的传染源和传播方式,从![]() 名确诊人员中随机抽出
名确诊人员中随机抽出![]() 人继续进行血清的研究,
人继续进行血清的研究,![]() 表示被抽取的
表示被抽取的![]() 人中
人中![]() 岁以下的人数,求
岁以下的人数,求![]() 的分布列以及数学期望.
的分布列以及数学期望.
参考表:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
参考公式: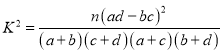 ,其中
,其中![]() .
.