题目内容
在以O为原点的直角坐标系中,点A(4,-3)为△OAB的直角顶点.已知|AB|=2|OA|,且点B的纵坐标大于零.(1)求向量![]() 的坐标;
的坐标;
(2)求圆x2-6x+y2+2y=0关于直线OB对称的圆的方程;
(3)是否存在实数a,使抛物线y=ax2-1上总有关于直线OB对称的两个点?若不存在,请说明理由;若存在,求a的取值范围.
解:(1)设![]() =(u,v),则由
=(u,v),则由
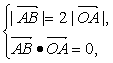 即
即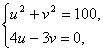 得
得![]() 或
或![]()
因为![]() =
=![]() +
+![]() =(u+4,v-3),
=(u+4,v-3),
所以v-3>0,得v=8.故![]() =(6,8).
=(6,8).
(2)由![]() =(10,5),得B(10,5),于是直线OB的方程为y=
=(10,5),得B(10,5),于是直线OB的方程为y=![]() x.
x.
由条件可知圆的标准方程为(x-3)2+(y+1)2=10,
得圆心(3,-1),半径为![]() .
.
设圆心(3,-1)关于直线OB的对称点为(x,y),则由
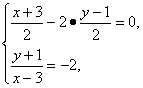
得![]()
故所求圆的方程为(x-1)2+(y-3)2=10.
(3)设P(x1,y1)、Q(x2,y2)为抛物线上关于直线OB对称的两点,
则有
解之得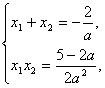
即x1、x2为方程x2+![]() x+
x+![]() =0的两个相异实根,
=0的两个相异实根,
于是由Δ=![]() -4·
-4·![]() >0,得a>
>0,得a>![]() .
.
故当a>![]() 时,抛物线y=ax2-1上总有关于直线OB对称的两点.
时,抛物线y=ax2-1上总有关于直线OB对称的两点.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目