题目内容
(03年上海卷)(14分)
在以O为原点的直角坐标系中,点A(4,-3)为△OAB的直角顶点.已知|AB|=2|OA|,且点B的纵坐标大于零.
(1)求向量![]() 的坐标;
的坐标;
(2)求圆![]() 关于直线OB对称的圆的方程;
关于直线OB对称的圆的方程;
(3)是否存在实数a,使抛物线![]() 上总有关于直线OB对称的两个点?若不存在,说明理由:若存在,求a的取值范围.
上总有关于直线OB对称的两个点?若不存在,说明理由:若存在,求a的取值范围.
解析:(1)设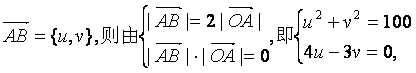 得
得
![]()
所以v-3>0,得v=8,故![]() ={6,8}.
={6,8}.
(2)由![]() ={10,5},得B(10,5),于是直线OB方程:
={10,5},得B(10,5),于是直线OB方程:![]()
由条件可知圆的标准方程为:(x-3)2+y(y+1)2=10, 得圆心(3,-1),半径为![]() .
.
设圆心(3,-1)关于直线OB的对称点为(x ,y)则
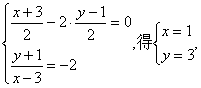 故所求圆的方程为(x-1)2+(y-3)2=10.
故所求圆的方程为(x-1)2+(y-3)2=10.
(3)设P (x1,y1), Q (x2,y2) 为抛物线上关于直线OB对称两点,则

故当![]() 时,抛物线y=ax2-1上总有关于直线OB对称的两点.
时,抛物线y=ax2-1上总有关于直线OB对称的两点.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目