题目内容
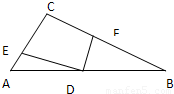
如图，P是Rt△ABC的斜边BC上异于B、C的一点，若过点P作直线l截△ABC，使截得的三角形与△ABC相似，则直线l共有（ ）分析：过点P作直线与另一边相交，使所得的三角形与原三角形有一个公共角，只要再作一个直角就可以．
解答：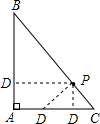
解：∵截得的三角形与△ABC相似，
∴过点P作AB的垂线，或作AC的垂线，或作BC的垂线，所得三角形满足题意
∴过点P作直线l共有三条，
故选C．
解：∵截得的三角形与△ABC相似，∴过点P作AB的垂线，或作AC的垂线，或作BC的垂线，所得三角形满足题意
∴过点P作直线l共有三条，
故选C．
点评：本题考查三角形相似的判定，考查合情推理，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
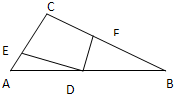（1）如图，D是Rt△ABC的斜边AB上的中点，E和F分别在边AC和BC上，且ED⊥FD，求证：EF2=AE2+BF2（EF2表示线段EF长度的平方）（尝试用向量法证明）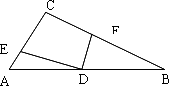
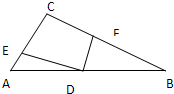（1）如图，D是Rt△ABC的斜边AB上的中点，E和F分别在边AC和BC上，且ED⊥FD，求证：EF2=AE2+BF2（EF2表示线段EF长度的平方）（尝试用向量法证明）
