题目内容
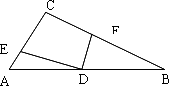
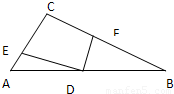
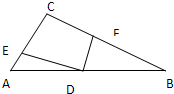 (1)如图,D是Rt△ABC的斜边AB上的中点,E和F分别在边AC和BC上,且ED⊥FD,求证:EF2=AE2+BF2(EF2表示线段EF长度的平方)(尝试用向量法证明)
(1)如图,D是Rt△ABC的斜边AB上的中点,E和F分别在边AC和BC上,且ED⊥FD,求证:EF2=AE2+BF2(EF2表示线段EF长度的平方)(尝试用向量法证明)
(2)已知函数f(x)=x3-3x图象上一点P(1,-2),过点P作直线l与y=f(x)图象相切,但切点异于点P,求直线l的方程.
 解:(1)连接EF,取EF的中点为G,
解:(1)连接EF,取EF的中点为G,又D是Rt△ABC的斜边AB上的中点,
∴
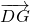 =
= +
+ +
+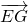 ,
,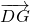 =
=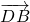 +
+ +
+ ,
,两式相加,注意到
 ,
, ,
,得
 ,又在直角三角形EFD中,
,又在直角三角形EFD中, ,
,故
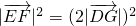 ,即
,即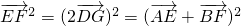
又AC⊥BC,展开上式即EF2=AE2+BF2
得证. (6分)
(其他方法也给分,向量的代数运算要引起学生的关注)
(2)设为(x0,y0)函数f(x)=x3-3x图象上任一点,
易得f′(x)=3x2-3,则
 ,
,故(x0,y0)处切线为
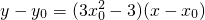
又知过P(1,-2)点,代入解方程得:x0=1(舍),

故所求直线的斜率
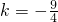 ,从而切线方程为:9x+4y-1=0(12分)
,从而切线方程为:9x+4y-1=0(12分)分析:(1)连接EF,取EF的中点为G,根据向量的加法法则得
 ,又
,又 ,从而有
,从而有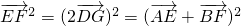 ,又AC⊥BC,展开上式即得证.
,又AC⊥BC,展开上式即得证. (2)由已知可得斜率函数为f′(x)=3x2-3,进而求出所过点切线的斜率,设另一切点为(x0,y0),代入点斜式公式,求出该点切线方程,再由条件计算.
点评:本题主要考查的是向量在几何中的应用、直线的点斜式方程的求解、导数的几何意义等,属于基础题.

练习册系列答案
相关题目
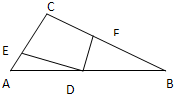 (1)如图,D是Rt△ABC的斜边AB上的中点,E和F分别在边AC和BC上,且ED⊥FD,求证:EF2=AE2+BF2(EF2表示线段EF长度的平方)(尝试用向量法证明)
(1)如图,D是Rt△ABC的斜边AB上的中点,E和F分别在边AC和BC上,且ED⊥FD,求证:EF2=AE2+BF2(EF2表示线段EF长度的平方)(尝试用向量法证明)