题目内容
在平面直角坐标系中,曲线C1的参数方程为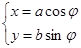 (a>b>0,
(a>b>0,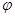 为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点M
为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点M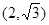 对应的参数
对应的参数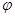 =
=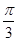 ,
,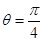 与曲线C2交于点D
与曲线C2交于点D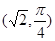
(1)求曲线C1,C2的方程;
(2)A(ρ1,θ),Β(ρ2,θ+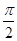 )是曲线C1上的两点,求
)是曲线C1上的两点,求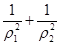 的值。
的值。
(1)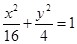 ,ρ=2cosθ(或(x 1)2+y2=1);(2)
,ρ=2cosθ(或(x 1)2+y2=1);(2) .
.
解析试题分析:本题主要考查参数方程与普通方程的互化、极坐标与直角坐标方程的互化、椭圆和圆的标准方程等基础知识,考查学生的转化能力和分析能力.第一问,将M点坐标及对应的参数代入曲线 中即可求出参数方程中的a和b,再写直角坐标方程;第二问,根据已知条件的描述知,圆心在x轴上,且过圆点,半径为R,即可写出圆的标准方程,而圆还过点D,代入点D的坐标即可求出R的值,即得到圆的方程;第二问,先写出曲线
中即可求出参数方程中的a和b,再写直角坐标方程;第二问,根据已知条件的描述知,圆心在x轴上,且过圆点,半径为R,即可写出圆的标准方程,而圆还过点D,代入点D的坐标即可求出R的值,即得到圆的方程;第二问,先写出曲线 的极坐标方程,将A、B点代入,进行等量代换即可.
的极坐标方程,将A、B点代入,进行等量代换即可.
(1)将M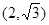 及对应的参数φ=
及对应的参数φ=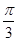 ,
,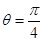 ;代入
;代入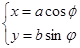 得
得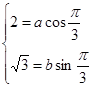 ,
,
所以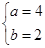 ,所以C1的方程为
,所以C1的方程为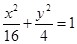 ,
,
设圆C2的半径R,则圆C2的方程为:ρ=2Rcosθ(或(x R)2+y2=R2),将点D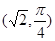 代入得:
代入得:
∴R=1 ∴圆C2的方程为:ρ=2cosθ(或(x 1)2+y2=1) 5分
(2)曲线C1的极坐标方程为: ,将A(ρ1,θ),Β(ρ2,θ+
,将A(ρ1,θ),Β(ρ2,θ+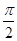 )代入得:
)代入得: ,
,
所以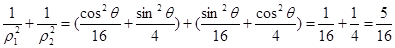
即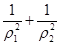 的值为
的值为 。 10分
。 10分
考点:参数方程与普通方程的互化、极坐标与直角坐标方程的互化、椭圆和圆的标准方程.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
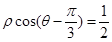 ,以极点O为原点,极轴Ox为x的非负半轴,保持单位长度不变建立直角坐标系xoy.
,以极点O为原点,极轴Ox为x的非负半轴,保持单位长度不变建立直角坐标系xoy.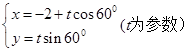 .若C与
.若C与 的交点为P,求点P与点A(-2,0)的距离|PA|.
的交点为P,求点P与点A(-2,0)的距离|PA|.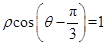 ,M,N分别为曲线C与x轴、y轴的交点.
,M,N分别为曲线C与x轴、y轴的交点.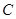 的极坐标方程为
的极坐标方程为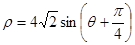 ,现以极点
,现以极点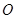 为原点,极轴为
为原点,极轴为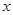 轴的非负半轴建立平面直角坐标系,直线
轴的非负半轴建立平面直角坐标系,直线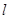 的参数方程为
的参数方程为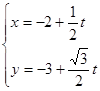 (
(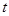 为参数)
为参数)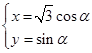 (α为参数).
(α为参数). ,判断点P与直线l的位置关系;
,判断点P与直线l的位置关系; sin
sin ,以极点为坐标原点、极轴为x轴正半轴建立平面直角坐标系,直线l的参数方程为
,以极点为坐标原点、极轴为x轴正半轴建立平面直角坐标系,直线l的参数方程为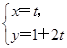 (t为参数),判断直线l和圆C的位置关系.
(t为参数),判断直线l和圆C的位置关系.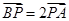 ,点P的轨迹为曲线C.
,点P的轨迹为曲线C.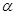 为参数,求曲线C的参数方程;
为参数,求曲线C的参数方程;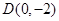 距离的最大值.
距离的最大值. (ρ∈R). (2)ρcos2
(ρ∈R). (2)ρcos2 =1.
=1.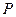 的极坐标为
的极坐标为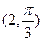 ,以极点为直角坐标系的原点,极轴为
,以极点为直角坐标系的原点,极轴为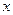 轴正半轴,建立直角坐标系,且在两种坐标系中取相同的长度单位,则
轴正半轴,建立直角坐标系,且在两种坐标系中取相同的长度单位,则