题目内容
在直角坐标系xOy中,直线l的方程为x-y+2=0,
曲线C的参数方程为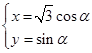 (α为参数).
(α为参数).
(1)已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为 ,判断点P与直线l的位置关系;
,判断点P与直线l的位置关系;
(2)设点Q是曲线C上的一个动点,求它到直线l的距离的最大值.
(1)点P在直线l上;(2)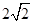 .
.
解析试题分析:(1)点极坐标系下的点P化为直角坐标,即可判断点P与直线l的关系;(2)点Q是曲线C上的动点,∴可设Q(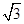 cosα,sinα),利用点到直线的距离公式,可以将Q到l的距离表示为
cosα,sinα),利用点到直线的距离公式,可以将Q到l的距离表示为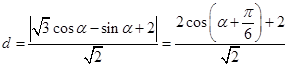 ,利用三角恒等变形,即可求得Q到直线l的最大距离.
,利用三角恒等变形,即可求得Q到直线l的最大距离.
(1)把极坐标系下的点P 化为直角坐标,得P(0,2). 3分
化为直角坐标,得P(0,2). 3分
因为点P的直角坐标(0,4)满足直线l的方程x-y+2=0,所以点P在直线l上. 4分
(2)因为点Q在曲线C上,故可设点Q的坐标为(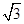 cosα,sinα),从而点Q到直经l的距离为
cosα,sinα),从而点Q到直经l的距离为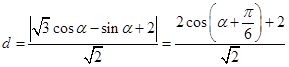 9分
9分
由此得,当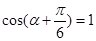 时,d取得最大值,且最大值为
时,d取得最大值,且最大值为 . 12分.
. 12分.
考点: 1、极坐标与直角坐标的互化;2、点到直线距离公式;3、三角恒等变形.

练习册系列答案
相关题目
 中,以
中,以 为极点,
为极点,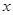 轴非负半轴为极轴建立坐标系,已知曲线
轴非负半轴为极轴建立坐标系,已知曲线 的极坐标方程为
的极坐标方程为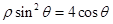 ,直线
,直线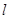 的参数方程为:
的参数方程为: 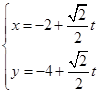 (
( 为参数),两曲线相交于
为参数),两曲线相交于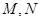 两点. 求:
两点. 求: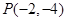 求
求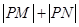 的值.
的值. 的直角坐标方程为
的直角坐标方程为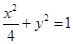 . 以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系. P是曲线
. 以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系. P是曲线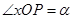 ,
,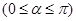 ,将点P绕点O逆时针旋转角
,将点P绕点O逆时针旋转角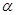 后得到点Q,
后得到点Q,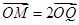 ,点M的轨迹是曲线
,点M的轨迹是曲线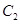 .
.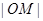 的取值范围.
的取值范围.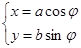 (a>b>0,
(a>b>0,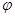 为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点M
为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点M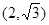 对应的参数
对应的参数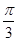 ,
,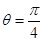 与曲线C2交于点D
与曲线C2交于点D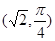
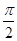 )是曲线C1上的两点,求
)是曲线C1上的两点,求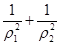 的值。
的值。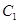 的极坐标方程是
的极坐标方程是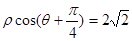 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为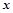 轴的正半轴,建立平面直角坐标系,曲线
轴的正半轴,建立平面直角坐标系,曲线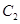 的参数方程是:
的参数方程是: (
(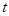 是参数).
是参数). 两点,求证
两点,求证 ;
;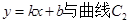 交于两点
交于两点 ,且
,且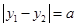 (
( 且
且 为常数),过弦
为常数),过弦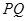 的中点
的中点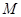 作平行于
作平行于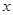 轴的直线交曲线
轴的直线交曲线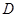 ,求证:
,求证: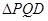 的面积是定值.
的面积是定值.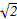 ρcos(θ-
ρcos(θ- )=2.
)=2. ,点B在直线
,点B在直线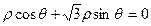 上运动,当线段AB最短时,点B的极坐标为__________。
上运动,当线段AB最短时,点B的极坐标为__________。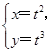 (t为参数)相交于A、B两点,求|AB|.
(t为参数)相交于A、B两点,求|AB|.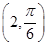 到直线ρsinθ=2的距离.
到直线ρsinθ=2的距离.