题目内容
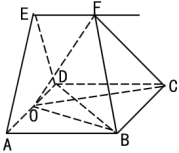
【题目】如图,在四棱柱![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形,![]() .
.
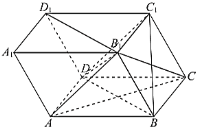
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() 是等边三角形,求点
是等边三角形,求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)连接![]() 交
交![]() 于点
于点![]() ,可知点
,可知点![]() 为
为![]() 的中点,利用等腰三角形三线合一的性质可得出
的中点,利用等腰三角形三线合一的性质可得出![]() ,利用菱形的性质可得出
,利用菱形的性质可得出![]() ,可得出
,可得出![]() 平面
平面![]() ,结合面面垂直的判定定理可得出结论;
,结合面面垂直的判定定理可得出结论;
(2)计算出![]() ,并推导出
,并推导出![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,进而可得出
,进而可得出![]() 到平面
到平面![]() 的距离与点
的距离与点![]() 到平面
到平面![]() 的距离相等,即为
的距离相等,即为![]() .
.
(1)如图,设![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,
,
因为四边形![]() 为菱形,故
为菱形,故![]() ,
,![]() 为
为![]() 的中点.
的中点.
又![]() ,故
,故![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,故
,故![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ;
;
(2)底面![]() 是边长为
是边长为![]() 的菱形,又
的菱形,又![]() ,所以
,所以![]() ,
,![]() .
.
又![]() 是等边三角形,可得
是等边三角形,可得![]() ,
,![]() ,
,![]() .
.
由(1)可知![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,则
,则![]() ,所以
,所以![]() .
.
设![]() 交
交![]() 于点
于点![]() ,
,

又![]() ,
,![]() ,所以平行四边形
,所以平行四边形![]() 为菱形,故
为菱形,故![]() .
.
又![]() ,
,![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,所以
,所以![]() .
.
![]() ,所以
,所以![]() 平面
平面![]() ,故
,故![]() 为
为![]() 在平面
在平面![]() 内的射影,故点
内的射影,故点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
又![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
故点![]() 到平面
到平面![]() 的距离与点
的距离与点![]() 到平面
到平面![]() 的距离相等,
的距离相等,
所以点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案【题目】自由购是通过自助结算方式购物的一种形式. 某大型超市为调查顾客使用自由购的情况,随机抽取了100人,统计结果整理如下:
20以下 |
|
|
|
|
| 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(Ⅰ)现随机抽取 1 名顾客,试估计该顾客年龄在![]() 且未使用自由购的概率;
且未使用自由购的概率;
(Ⅱ)从被抽取的年龄在![]() 使用自由购的顾客中,随机抽取3人进一步了解情况,用
使用自由购的顾客中,随机抽取3人进一步了解情况,用![]() 表示这3人中年龄在
表示这3人中年龄在![]() 的人数,求随机变量
的人数,求随机变量![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)为鼓励顾客使用自由购,该超市拟对使用自由购的顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋.
【题目】2019年10月1日我国隆重纪念了建国70周年,期间进行了一系列大型庆祝活动,极大地激发了全国人民的爱国热情.某校高三学生也投入到了这场爱国活动中,他(她)们利用周日休息时间到社区做义务宣讲员,学校为了调查高三男生和女生周日的活动时间情况,随机抽取了高三男生和女生各40人,对他(她)们的周日活动时间进行了统计,分别得到了高三男生的活动时间(单位:小时)的频数分布表和女生的活动时间(单位:小时)的频率分布直方图.(活动时间均在![]() 内)
内)
活动时间 |
|
|
|
|
|
|
频数 | 8 | 10 | 7 | 9 | 4 | 2 |
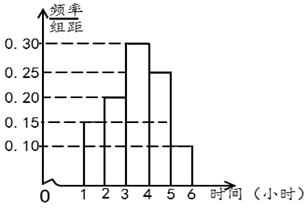
(1)根据调查,试判断该校高三年级学生周日活动时间较长的是男生还是女生?并说明理由;
(2)在被抽取的80名高三学生中,从周日活动时间在![]() 内的学生中抽取2人,求恰巧抽到1男1女的概率.
内的学生中抽取2人,求恰巧抽到1男1女的概率.