题目内容
已知数列 为递减的等差数列,
为递减的等差数列,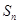 是数列
是数列 的前
的前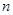 项和,且
项和,且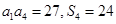 .
.
⑴ 求数列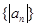 的前
的前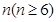 项和
项和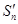
⑵ 令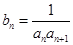 ,求数列
,求数列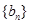 的前
的前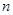 项和
项和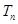
⑴当 时,
时, ;⑵
;⑵
解析试题分析:⑴∵ ,又∵
,又∵ ,
, ,
,
∴ ,∴
,∴ ,∴
,∴
∴当 时,
时, ;
;
⑵∵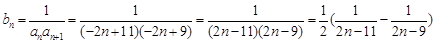

考点:本题主要考查等差数列的概念及其通项公式,数列的求和。
点评:典型题,“裂项相消法”求数列的前n项和属于常考题目,本题解答首先确定数列的通项公式是关键。

练习册系列答案
相关题目
题目内容
已知数列 为递减的等差数列,
为递减的等差数列,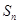 是数列
是数列 的前
的前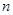 项和,且
项和,且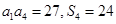 .
.
⑴ 求数列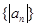 的前
的前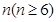 项和
项和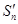
⑵ 令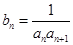 ,求数列
,求数列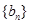 的前
的前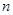 项和
项和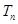
⑴当 时,
时, ;⑵
;⑵
解析试题分析:⑴∵ ,又∵
,又∵ ,
, ,
,
∴ ,∴
,∴ ,∴
,∴
∴当 时,
时, ;
;
⑵∵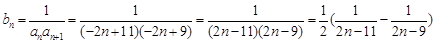

考点:本题主要考查等差数列的概念及其通项公式,数列的求和。
点评:典型题,“裂项相消法”求数列的前n项和属于常考题目,本题解答首先确定数列的通项公式是关键。
