题目内容
(满分14分)设函数![]() 的定义域是R,对于任意实数
的定义域是R,对于任意实数![]() ,恒有
,恒有
![]() ,且当
,且当![]() 时,
时,![]() 。
。
⑴求证:![]() ,且当
,且当![]() 时,有
时,有![]() ;
;
⑵判断![]() 在R上的单调性;
在R上的单调性;
⑶设集合![]() ,集合
,集合![]() ,若A∩B=
,若A∩B=![]() ,求a的取值范围。
,求a的取值范围。
解:⑴f(m+n)=f(m)f(n),令m=1,n=0,则f(1)=f(1)f(0),且由x>0时,0<f(x)<1,∴f(0)=1;设m=x<0,n=-x>0,∴f(0)=f(x)f(-x),∴f(x)=![]() >1。
>1。
⑵设x1<x2,则x2-x1>0,∴0<f(x2-x1)<1,∴f(x2)-f(x1)=f[(x2-x1)+x1]-f(x1)=f(x2-x1)f(x1)-f(x1)=f(x1)[f(x2-x1)-1]<0,∴f(x)在R上单调递减。
⑶∵f(x2)f(y2)>f(1),∴f(x2+y2)>f(1),由f(x)单调性知x2+y2<1,又f(ax-y+2)=1=f(0),
∴ax-y+2=0,又A∩B=![]() ,∴
,∴![]() ,∴a2+1≤4,从而
,∴a2+1≤4,从而![]() 。
。

练习册系列答案
相关题目

 ,其中
,其中
 判断
判断 在
在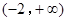 上的单调性.
上的单调性. ,
, ,当
,当 时,
时,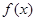 取得极值。
取得极值。 的值;
的值; 时,函数
时,函数 的图象有三个公共点,求
的图象有三个公共点,求 的取值范围。
的取值范围。