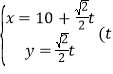题目内容
【题目】如图,在棱长为2的正方体![]() 中,点
中,点![]() 分别是棱
分别是棱![]() 上的动点,且
上的动点,且![]() .
.
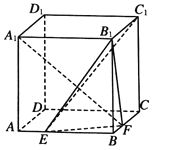
(1)求证:![]() ;
;
(2)当三棱锥![]() 的体积取得最大值时,求二面角
的体积取得最大值时,求二面角![]() 的正切值.
的正切值.
【答案】(1)见证明;(2)![]()
【解析】
设AE=BF=x.以D为原点建立空间直角坐标系,求出相关点的坐标
(1)通过计算![]() ,证明A1F⊥C1E.
,证明A1F⊥C1E.
(2)判断当S△BEF取得最大值时,三棱锥B1﹣BEF的体积取得最大值.求出平面B1EF的法向量,底面ABCD的法向量,设二面角B1﹣EF﹣B的平面角为θ,利用空间向量的数量积求出![]() ,然后求解二面角B1﹣EF﹣B的正切值.
,然后求解二面角B1﹣EF﹣B的正切值.
设AE=BF=x.以D为原点建立空间直角坐标系,得下列坐标:D(0,0,0),A(2,0,0),B(2,2,0),C(0,2,0),D1(0,0,2),A1(2,0,2),B1(2,2,2),C1(0,2,2),E(2,x,0),F(2﹣x,2,0).
(1)因为![]() ,
,![]() ,
,
所以![]() .
.
所以A1F⊥C1E.

(2)因为![]() ,
,
所以当S△BEF取得最大值时,三棱锥B1﹣BEF的体积取得最大值.
因为![]() ,
,
所以当x=1时,即E,F分别是棱AB,BC的中点时,三棱锥B1﹣BEF的体积取得最大值,此时E,F坐标分别为E(2,1,0),F(1,2,0).
设平面B1EF的法向量为![]() ,
,
则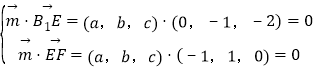 得
得![]()
取a=2,b=2,c=﹣1,得![]() .显然底面ABCD的法向量为
.显然底面ABCD的法向量为![]() .
.
设二面角B1﹣EF﹣B的平面角为θ,由题意知θ为锐角.
因为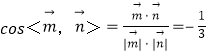 ,所以
,所以![]() ,于是
,于是![]() .
.
所以![]() ,即二面角B1﹣EF﹣B的正切值为
,即二面角B1﹣EF﹣B的正切值为![]() .
.

【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了各级城市的大街小巷,为了解我市的市民对共享单车的满意度,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了50人进行分析.若得分低于60分,说明不满意,若得分不低于60分,说明满意,调查满意度得分情况结果用茎叶图表示如图1.
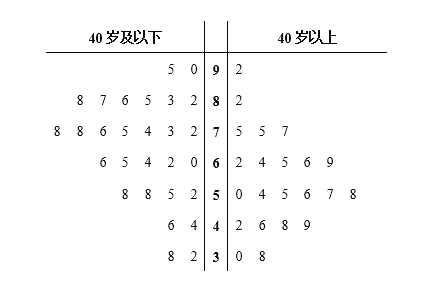
(Ⅰ)根据茎叶图找出40岁以上网友中满意度得分的众数和中位数;
(Ⅱ)根据茎叶图完成下面列联表,并根据以上数据,判断是否有![]() 的把握认为满意度与年龄有关;
的把握认为满意度与年龄有关;
满意 | 不满意 | 合计 | |
40岁以下 | |||
40岁以上 | |||
合计 |
(Ⅲ)先采用分层抽样的方法从40岁及以下的网友中选取7人,再从这7人中随机选出2人,将频率视为概率,求选出的2人中至少有1人是不满意的概率.
参考格式: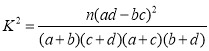 ,其中
,其中![]()
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |