题目内容
 已知四棱锥P-ABCD中,点M是PC的中点,点E是AB上的一个动点,且该四棱锥的三视图如图所示,其中正视图和侧视图是直角三角形.
已知四棱锥P-ABCD中,点M是PC的中点,点E是AB上的一个动点,且该四棱锥的三视图如图所示,其中正视图和侧视图是直角三角形.(I)求证:PA∥平面BDM;
(II)若点E是AB的中点,求证:CE⊥平面PDE;
(III)无论点E在何位置,是否均有三棱锥C-PDE的体积为定值?若是,请求出定值;若不是,请说明理由.
分析:(I)连接AC,交BD于点O,连接OM,PE,由三视图可知,四边形ABCD为矩形,可证MO∥PA,根据线面平行的判定定理可证
(II)由三视图可知,PD⊥平面ABCD,AD=PD=1,AB=2,PD⊥CE,则△ADE与△BCE都是等腰直角三角形即∠AED+∠BEC=90°,则CE⊥DE,根据线面垂直的判定定理可证
III)VP-CDE=VC-PDE=
×PD×S△CDE,即可
(II)由三视图可知,PD⊥平面ABCD,AD=PD=1,AB=2,PD⊥CE,则△ADE与△BCE都是等腰直角三角形即∠AED+∠BEC=90°,则CE⊥DE,根据线面垂直的判定定理可证
III)VP-CDE=VC-PDE=
| 1 |
| 3 |
解答:证明:(I)连接AC,交BD于点O,连接OM,PE
由三视图可知,四边形ABCD为矩形
∴O是AC的中点
又∵M是PC的中点
在PAC中,则MO∥PA(2分)
由MO?平面BDM,PA?面BDM(3分)
∴PA∥面BDM(4分)
(II)由三视图可知,PD⊥平面ABCD,AD=PD=1,AB=2
∵CE?面ABCD,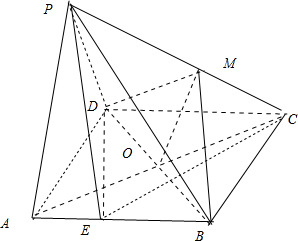
∴PD⊥CE(6分)
∵E为AB的中点
∴△ADE与△BCE都是等腰直角三角形
∴∠AED+∠BEC=90°
∴CE⊥DE(8分)
∵PD∩DE=D
∴CE⊥面PDE(9分)
III)VP-CDE=VC-PDE=
×PD×S△CDE
∵无论点E在任何位置,△CDE的面积均为定值
即S△CDE=
•CD•AD=
×2×1=1(10分)
∴VC-PDE=
×1×1=
(12分)
由三视图可知,四边形ABCD为矩形
∴O是AC的中点
又∵M是PC的中点
在PAC中,则MO∥PA(2分)
由MO?平面BDM,PA?面BDM(3分)
∴PA∥面BDM(4分)
(II)由三视图可知,PD⊥平面ABCD,AD=PD=1,AB=2
∵CE?面ABCD,

∴PD⊥CE(6分)
∵E为AB的中点
∴△ADE与△BCE都是等腰直角三角形
∴∠AED+∠BEC=90°
∴CE⊥DE(8分)
∵PD∩DE=D
∴CE⊥面PDE(9分)
III)VP-CDE=VC-PDE=
| 1 |
| 3 |
∵无论点E在任何位置,△CDE的面积均为定值
即S△CDE=
| 1 |
| 2 |
| 1 |
| 2 |
∴VC-PDE=
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题主要考查了线面平行与线面垂直的判定定理的应用,注意线线关系与线面关系的相互转化,及利用换定点求解三棱锥的体积.

练习册系列答案
相关题目
 如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点.
如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点. 如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点.
如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点. 已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,AB=BC=2CD=2,BD⊥PE.
已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,AB=BC=2CD=2,BD⊥PE. 如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是线段PC上一点,PC⊥平面BDE.
如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是线段PC上一点,PC⊥平面BDE.