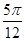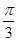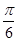题目内容
正四棱锥的侧棱长与底面边长都是1,则侧棱与底面所成的角为( )
| A.75° | B.60° | C.45° | D.30° |
C
解析试题分析:如图,四棱锥P-ABCD中,过P作PO⊥平面ABCD于O,连接AO,则AO是AP在底面ABCD上的射影.∴∠PAO即为所求线面角,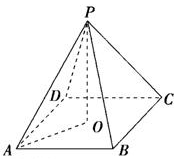
∵AO=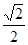 ,PA=1,∴cos∠PAO=
,PA=1,∴cos∠PAO=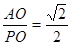 ,.∴∠PAO=45°,即所求线面角为45°.故答案为C.
,.∴∠PAO=45°,即所求线面角为45°.故答案为C.
考点:直线与平面所成的角;棱锥的结构特征.
点评:本题考查棱锥的结构特征,以及求直线和平面成的角的方法,体现了数形结合的数学思想.

练习册系列答案
相关题目
设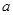 、
、 是不同的直线,
是不同的直线, 、
、 是不同的平面,则下列命题:
是不同的平面,则下列命题:
①若 ,则
,则 ;②若
;②若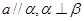 ,则
,则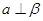 ;
;
③若 ,则
,则 ;④若
;④若 ,则
,则 .
.
其中正确命题的个数是( )
| A.0 | B.1 | C.2 | D.3 |
设平面 与平面
与平面 相交于直线
相交于直线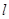 ,直线
,直线 在平面
在平面 内,直线
内,直线 在平面
在平面 内,且
内,且 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
设m,n是两条不同的直线, 是三个不同的平 面,则下列为假命题的是
是三个不同的平 面,则下列为假命题的是
A.若 ,则 ,则 |
B.若 |
C.若 |
D.若 |
在空间,下列命题正确的是
| A.平行直线的平行投影重合 | B.平行于同一直线的两个平面平行 |
| C.垂直于同一平面的两个平面平行 | D.垂直于同一平面的两条直线平行 |
设 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,则下列四个命题中,正确命题的个数是( )
是两个不同的平面,则下列四个命题中,正确命题的个数是( )
①若 ②若
②若
③若 ④若
④若
| A.3个 | B.2个 | C.1个 | D.0个 |
下列命题中假命题是
| A.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行 |
| B.垂直于同一条直线的两条直线相互垂直 |
| C.若一个平面经过另一个平面的垂线,那么这两个平面相互垂直 |
| D.若一个平面内的两条相交直线与另一个平面内的相交直线分别平行,那么这两个平面相互平行 |
已知正四棱柱 中,
中, ,则CD与平面
,则CD与平面 所成角的正弦值等于( )
所成角的正弦值等于( )
A. | B. | C. | D. |
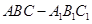 的侧棱与底面垂直,体积为
的侧棱与底面垂直,体积为 ,底面是边长为
,底面是边长为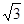 的正三角形,若
的正三角形,若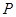 为底面
为底面 的中心,则
的中心,则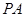 与平面
与平面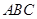 所成角的大小为( )
所成角的大小为( )