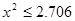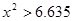题目内容
为调查某地区大学生是否爱好某项体育运动,用简单随机抽样方法从该地区的大学里调查了500位大学生,结果如下:
| | 男 | 女 |
| 爱好 | 40 | 30 |
| 不爱好 | 160 | 270 |
(2) 能否有99%的把握认为该地区的大学生是否爱好该项体育运动与性别有关?
附:
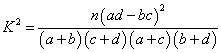
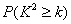 | 0.050 | 0.010 | 0.001 |
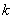 | 3.841 | 6.635 | 10.828 |
(1)14%(2)有关
解析试题分析:解:(1)调查的500位大学生中有70位爱好这项体育运动,因此该地区大学生中,,爱好该项运动的大学生的比例为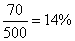
(2)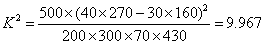 。
。
由于9.967>6.635,所以有99%的把握认为该地区的大学生是否爱好该项体育运动与性别有关。
考点:独立性检验
点评:解决关于独立性检验问题的步骤:第一步:提出假设检验问题;第二步:选择检验的指标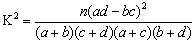 ;第三步:查表得出结论。
;第三步:查表得出结论。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在一段时间内,某种商品价格 (万元)和需求量
(万元)和需求量 之间的一组数据为:
之间的一组数据为:
价 格 | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
需求量 | 12 | 10 | 7 | 5 | 3 |
(2)如果
 与
与 之间具有线性相关关系,求出回归直线方程,并预测当价格定为1.9万元,需求量大约是多少?(精确到0.01
之间具有线性相关关系,求出回归直线方程,并预测当价格定为1.9万元,需求量大约是多少?(精确到0.01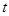 )
)参考公式及数据:
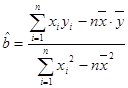 ,
,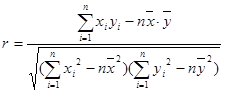 ,
,
相关性检验的临界值表:
| n-2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 小概率0.01 | 1.000 | 0.990 | 0.959 | 0.917 | 0.874 | 0.834 | 0.798 | 0.765 | 0.735 | 0.708 |
有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下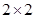 联表:
联表:
| | 优秀 | 非优秀 | 合计 |
| 甲班 | 30 | | |
| 乙班 | | 50 | |
| 合计 | | | 200 |
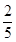
(1)请完成上面
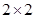 联表;
联表;(2)根据列联表的数据,能否有
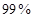 的把握认为“成绩与班级有关系”
的把握认为“成绩与班级有关系”(3)从全部200人中有放回抽取3次,每次抽取一人,记被抽取的3人中优秀的人数为
 ,若每次抽取得结果是相互独立的,求
,若每次抽取得结果是相互独立的,求 的分布列,期望
的分布列,期望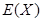 和方差
和方差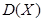
参考公式与参考数据如下:

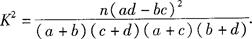
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(1)根据以上数据建立一个 的列联表;
的列联表;
(2)判断性别与休闲方式是否有关系。
(本题可以参考两个分类变量x和y有关系的可信度表:)
| P(k2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.83 |
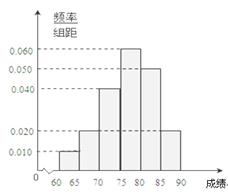
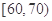 的考生中任抽取2人,求成绩在
的考生中任抽取2人,求成绩在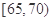 的考生至少有一人的概率.
的考生至少有一人的概率.
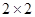 列联表:
列联表: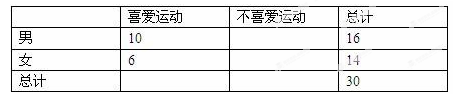
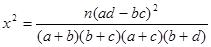 (其中
(其中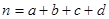 )
)