题目内容
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(1)根据以上数据建立一个 的列联表;
的列联表;
(2)判断性别与休闲方式是否有关系。
(本题可以参考两个分类变量x和y有关系的可信度表:)
| P(k2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.83 |
(1) 列联表为
列联表为
(2) 看电视 运动 合计 女 43 27 70 男 21 33 54 合计 64 60 124  97.5%的把握认为休闲方式与性别有关
97.5%的把握认为休闲方式与性别有关
解析试题分析:解:(1) 列联表为
列联表为
(2)假设“休闲方式与性别无关”,计算得到 看电视 运动 合计 女 43 27 70 男 21 33 54 合计 64 60 124 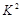 的观察值
的观察值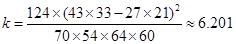
因为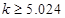 ,所以有理由认为假设“休闲方式与性别无关”是不合理的,即
,所以有理由认为假设“休闲方式与性别无关”是不合理的,即
有 97.5%的把握认为休闲方式与性别有关。
97.5%的把握认为休闲方式与性别有关。
考点:独立性检验的运用
点评:解决的关键是根据独立性检验的公式来求解得到,属于基础题。

为调查某地区大学生是否爱好某项体育运动,用简单随机抽样方法从该地区的大学里调查了500位大学生,结果如下:
| | 男 | 女 |
| 爱好 | 40 | 30 |
| 不爱好 | 160 | 270 |
(2) 能否有99%的把握认为该地区的大学生是否爱好该项体育运动与性别有关?
附:
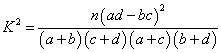
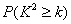 | 0.050 | 0.010 | 0.001 |
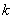 | 3.841 | 6.635 | 10.828 |
某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100棵种子中的发芽数,得到如下资料:
| 日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
| 温差x(℃) | 10 | 11 | 13 | 12 | 8 |
| 发芽y(颗) | 23 | 25 | 30 | 26 | 16 |
回归直线方程参考公式:

 ,
, 

(1)请根据12月2日至12月4日的数据,求出y关于x的线性回归方程
 ;
;(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则
认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
(3)请预测温差为14℃的发芽数。
某校的研究性学习小组为了研究高中学生的身体发育状况,在该校随机抽出120名17至18周岁的男生,其中偏重的有60人,不偏重的也有60人。在偏重的60人中偏高的有40人,不偏高的有20人;在不偏重的60人中偏高和不偏高人数各占一半
(1)根据以上数据建立一个 列联表:
| | 偏重 | 不偏重 | 合计 |
| 偏高 | | | |
| 不偏高 | | | |
| 合计 | | | |
通过随机询问110名性别不同的行人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如下的列联表:
| | 男 | 女 | 总计 |
| 走天桥 | 40 | 20 | |
| 走斑马线 | 20 | 30 | |
| 总计 | | | |
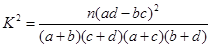 )
) | 0.050 0.010 0.001 |
 | 3.841 6.635 10.828 |
(2)能否在犯错误的概率不超过0.010的前提下认为性别与愿意走斑马线还是愿意走人行天桥有关系。
下表提供了某厂节能降耗技术发行后,生产甲产品过程中记录的产量 (吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
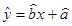 所表示的直线必经过的点;
所表示的直线必经过的点;(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
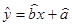 ;
;并预测生产1000吨甲产品的生产能耗多少吨标准煤?
(参考:
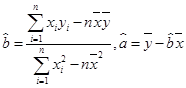 )
) (本小题共12分)
现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了50人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
| 月收入(单位百元) | [15,25 | [25,35 | [35,45 | [45,55 | [55,65 | [65,75 |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
(1)由以上统计数据填下面2乘2列联表并问是否有99%的把握认为“月收入以5500为分界点对“楼市限购令” 的态度有差异;
| | 月收入不低于55百元的人数 | 月收入低于55百元的人数 | 合计 |
| 赞成 |  |  | |
| 不赞成 |  |  | |
| 合计 | | | |
(2)若对在[15,25) ,[25,35)的被调查中各随机选取两人进行追踪调查,记选中的4人中不赞成“楼市限购令”人数为
 ,求随机变量
,求随机变量 的分布列。
的分布列。附: