题目内容
在一段时间内,某种商品价格 (万元)和需求量
(万元)和需求量 之间的一组数据为:
之间的一组数据为:
价 格 | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
需求量 | 12 | 10 | 7 | 5 | 3 |
(2)如果
 与
与 之间具有线性相关关系,求出回归直线方程,并预测当价格定为1.9万元,需求量大约是多少?(精确到0.01
之间具有线性相关关系,求出回归直线方程,并预测当价格定为1.9万元,需求量大约是多少?(精确到0.01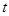 )
)参考公式及数据:
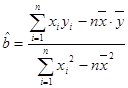 ,
,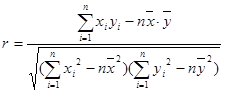 ,
,
相关性检验的临界值表:
| n-2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 小概率0.01 | 1.000 | 0.990 | 0.959 | 0.917 | 0.874 | 0.834 | 0.798 | 0.765 | 0.735 | 0.708 |
(1)从而有99%的把握认为 与
与 之间具有线性相关关系(2)
之间具有线性相关关系(2) ,当价格定为
,当价格定为 万元时,需求量大约为
万元时,需求量大约为
解析试题分析:(1)①作统计假设: 与
与 不具有线性相关关系。 1分
不具有线性相关关系。 1分
②由小概率0.01与 在附表中查得:
在附表中查得: 2分
2分
③ ,
, 3分
3分 4分
4分 5分
5分 6分
6分
∴
④ ,即
,即
从而有99%的把握认为 与
与 之间具有线性相关关系,去求回归直线方程是有意义的。 8分
之间具有线性相关关系,去求回归直线方程是有意义的。 8分
(2)回归系数  ,
,
∴ 对
对 的回归直线方程是
的回归直线方程是
当 时,
时, 。
。
这说明当价格定为 万元时,需求量大约为
万元时,需求量大约为 。 12分
。 12分
考点:相关性检验与回归方程
点评:求回归方程主要是将已知数据代入公式计算出 ;相关性检验的步骤:写出列联表,求出观测值
;相关性检验的步骤:写出列联表,求出观测值 ,观测值与边界值比较得结论
,观测值与边界值比较得结论

某初级中学共有学生2000名,各年级男、女生人数如下表:
| | 初一年级 | 初二年级 | 初三年级 |
| 女生 | 373 | 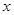 | 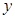 |
| 男生 | 377 | 370 | 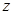 |
(1)求
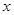 的值;
的值;(2)现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,下表为抽样试验的结果:
| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y(件) | 11 | 9 | 8 | 5 |
画出散点图,并通过散点图确定变量y对x是否线性相关;
(2)如果y对x有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么机器的运转速度应控制在什么范围内?(精确到0.0001)
某中学号召本校学生在本学期参加市创办卫生城的相关活动,学校团委对该校学生是否关心创卫活动用简单抽样方法调查了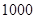 位学生(关心与不关心的各一半),
位学生(关心与不关心的各一半),
结果用二维等高条形图表示,如图.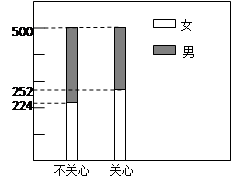
(1)完成列联表,并判断能否有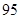 ℅的把握认为是否关心创卫活动与性别有关?
℅的把握认为是否关心创卫活动与性别有关?
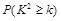 | 0.10 | 0.05 | 0.01 |
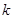 | 2.706 | 3.841 | 6.635 |
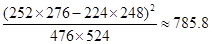
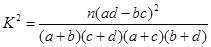 ;
;| | 女 | 男 | 合计 |
| 关心 | | | 500 |
| 不关心 | | | 500 |
| 合计 | | 524 | 1000 |
(2)已知校团委有青年志愿者100名,他们已参加活动的情况记录如下:
| 参加活动次数 | 1 | 2 | 3 |
| 人数 | 10 | 50 | 40 |
(i)从志愿者中任选两名学生,求他们参加活动次数恰好相等的概率;
(ii)从志愿者中任选两名学生,用
 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望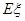 .
. 为调查某地区大学生是否爱好某项体育运动,用简单随机抽样方法从该地区的大学里调查了500位大学生,结果如下:
| | 男 | 女 |
| 爱好 | 40 | 30 |
| 不爱好 | 160 | 270 |
(2) 能否有99%的把握认为该地区的大学生是否爱好该项体育运动与性别有关?
附:
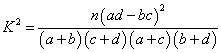
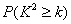 | 0.050 | 0.010 | 0.001 |
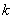 | 3.841 | 6.635 | 10.828 |
某校的研究性学习小组为了研究高中学生的身体发育状况,在该校随机抽出120名17至18周岁的男生,其中偏重的有60人,不偏重的也有60人。在偏重的60人中偏高的有40人,不偏高的有20人;在不偏重的60人中偏高和不偏高人数各占一半
(1)根据以上数据建立一个 列联表:
| | 偏重 | 不偏重 | 合计 |
| 偏高 | | | |
| 不偏高 | | | |
| 合计 | | | |
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(1)根据以上数据建立一个2×2的列联表;
(2)判断性别与休闲方式是否有关系。
附:
 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
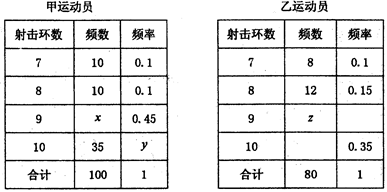
 表示这3次射击中击中9环以上(含9环)的次数,求
表示这3次射击中击中9环以上(含9环)的次数,求
