��Ŀ����
����Ŀ��
��֪��Բ![]() ���
���![]() ����ֱ��
����ֱ��![]() ���У���ԲԲ��
���У���ԲԲ��![]() �Ĺ켣��Ϊ
�Ĺ켣��Ϊ![]() ��ֱ��
��ֱ��![]() ��
��![]() ��Ľ���Ϊ
��Ľ���Ϊ![]() ������
������![]() ��б��Ϊ
��б��Ϊ![]() ��ֱ��
��ֱ��![]() ��켣
��켣![]() ��������ͬ�Ĺ�����
��������ͬ�Ĺ�����![]() ��
�� ![]() ��
�� ![]() Ϊ����ԭ��.
Ϊ����ԭ��.
��1����ԲԲ��![]() �Ĺ켣
�Ĺ켣![]() �ķ��̣�����ֱ��
�ķ��̣�����ֱ��![]() ��б��
��б��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����![]() �ǹ켣
�ǹ켣![]() ������
������![]() ��
�� ![]() ������һ�㣬ֱ��
������һ�㣬ֱ��![]() ��
�� ![]() �ֱ����
�ֱ����![]() �Ҵ�ֱ��
�Ҵ�ֱ��![]() ���ֱ�߽���
���ֱ�߽���![]() ��
�� ![]() ��֤����
��֤���� ![]() Ϊ��ֵ��������ö�ֵ��
Ϊ��ֵ��������ö�ֵ��
��3�����ڣ�2������һ����ۣ�����![]() ��ֱ��
��ֱ��![]() �������������䣬��
�������������䣬��![]() ��ֵ������ֱ��д�������.
��ֵ������ֱ��д�������.
���𰸡���1��![]() ��2��
��2��![]()
��������������������������ߵĶ����֪Բ�ĵĹ켣Ϊ�����ߣ���������ߵķ��̣�����ֱ�ߺ������߷��̣����������ó�����![]() ��һԪ���η��̣����ø���ϵ����ϵ�ó�
��һԪ���η��̣����ø���ϵ����ϵ�ó�![]() ��
��![]() ������ֱ�������������������㣬���
������ֱ�������������������㣬���![]() �ķ�Χ��д��
�ķ�Χ��д��![]() ���̣����
���̣����![]() ���꣬��ʾ
���꣬��ʾ![]() �����������.
�����������.
���������
��1���ɶ�Բ![]() ���
���![]() ����ֱ��
����ֱ��![]() ���еã���
���еã���![]() ��
��![]() �뵽ֱ��
�뵽ֱ��![]() ������ȣ�����Բ��
������ȣ�����Բ��![]() �Ĺ켣
�Ĺ켣![]() �ķ���Ϊ��
�ķ���Ϊ�� ![]()
����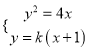 �ã�
�ã� ![]() ��
�� 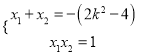
��![]() ʱ��һ�η���ֻ��һ���������Բ�����.
ʱ��һ�η���ֻ��һ���������Բ�����.
����![]() ���
���![]()
��֮��ֱ��![]() ��б��
��б��![]() ��ȡֵ��ΧΪ
��ȡֵ��ΧΪ![]()
��2����![]() ��
�� ![]() ��
�� ![]() ��
��
ֱ��![]() ��
�� ![]() ����
����![]() ��
�� ![]()
����![]() �Ľ���
�Ľ���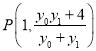 ��
��
ͬ��![]() ��
��![]() �Ľ���
�Ľ���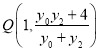
����![]()
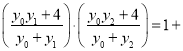
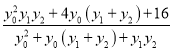
�ɣ�1���е�![]() �ã�
�ã� ![]() ������ʽ��
������ʽ��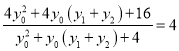
��![]()
![]()
��3����֤������Ҫ��ֻ�����۷�.
������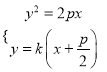 �ã�
�ã� ![]()
![]() ����
����![]() ����
����![]()
![]()
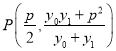 ��
�� 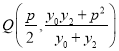
����![]()
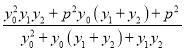
![]() ��
�� ![]()

 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�