题目内容
【题目】如图,在三棱锥P﹣ABC中,PA⊥AC,PA⊥AB,PA=AB,![]() ,
,![]() ,点D,E分别在棱PB,PC上,且DE∥BC,
,点D,E分别在棱PB,PC上,且DE∥BC,
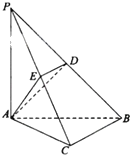
(1)求证:BC⊥平面PAC;
(2)当D为PB的中点时,求AD与平面PAC所成的角的正弦值.
【答案】(1)证明见解析(2)![]() .
.
【解析】
解法一:
(1)根据线面垂直的判定定理由已知的垂直的关系,可得到线面垂直,这样可以得到线线垂直,最后根据直角和线面垂直的判定定理证明出BC⊥平面PAC;
(2)结合(1)的结论、已知的平行线,根据线面角的定义,通过计算求出AD与平面PAC所成的角的正弦值.
解法二:建立空间直角坐标系.
(1)利用空间向量的数量积运用,证明线线垂直,再结合已知的垂直关系证明出线面垂直;
(2)利用空间向量夹角公式,求出AD与平面PAC所成的角的正弦值.
(解法一):(1)∵PA⊥AC,PA⊥AB,AC∩AB=A,
∴PA⊥底面ABC,
∴PA⊥BC.又∠BCA=90°,
∴AC⊥BC.
∴BC⊥平面PAC.
(2)∵D为PB的中点,DE∥BC,
∴DE![]() BC,
BC,
又由(1)知,BC⊥平面PAC,
∴DE⊥平面PAC,垂足为点E.
∴∠DAE是AD与平面PAC所成的角,
∵PA⊥底面ABC,
∴PA⊥AB,又PA=AB,
∴△ABP为等腰直角三角形,
∴AD![]() AB,
AB,
∴在Rt△ABC中,∠ABC=60°,
∴BC![]() AB.
AB.
∴在Rt△ADE中,sin∠DAE![]() ,
,
∴AD与平面PAC所成的角的正弦值是![]() .
.
(解法二):如图,以A为原点建立空间直角坐标系A﹣xyz,设PA=a,
由已知可得P(0,0,a),A(0,0,0),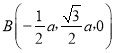 ,
,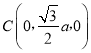 .
.
(1)∵![]() ,
,![]() ,
,
∴![]() ,
,
∴BC⊥AP.
又∵∠BCA=90°,
∴BC⊥AC,
∴BC⊥平面PAC.
(2)∵D为PB的中点,DE∥BC,
∴E为PC的中点,
∴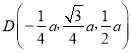 ,
,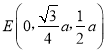 ,
,
∴又由(1)知,BC⊥平面PAC,
∴DE⊥平面PAC,垂足为点E.
∴∠DAE是AD与平面PAC所成的角,
∵![]() (
(![]() ),
),![]() (0,
(0,![]() a,
a,![]() a),
a),
∴cos∠DAE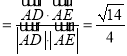 ,sin∠DAE
,sin∠DAE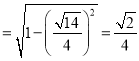 .
.
∴AD与平面PAC所成的角的正弦值为![]() .
.



