题目内容
某单位 名员工参加“社区低碳你我他”活动.他们的年龄在
名员工参加“社区低碳你我他”活动.他们的年龄在 岁至
岁至 岁
岁
之间.按年龄分组:第1组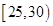 ,第
,第 组
组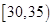 ,第3组
,第3组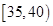 ,第
,第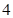 组
组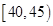 ,第
,第 组
组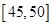 ,得到的频率分布直方图如图所示.下表是年龄的频率分布表.
,得到的频率分布直方图如图所示.下表是年龄的频率分布表.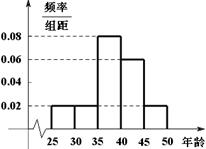
| 区间 | 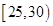 | 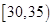 | 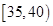 | 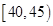 | 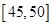 |
| 人数 |  |  |  | | |
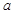 、
、 、
、 的值;
的值;(2)现要从年龄较小的第
 、
、 、
、 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取 人,则年龄在第
人,则年龄在第 、
、 、
、 组的人数分别
组的人数分别是多少?
(3)在(2)的条件下,从这
 人中随机抽取
人中随机抽取 人参加社区宣传交流活动,求恰有
人参加社区宣传交流活动,求恰有 人在第
人在第 组的概率.
组的概率.
(1)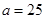 ,
,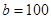 ,
,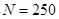 ;(2)
;(2) 、
、 、
、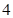 ;(3)
;(3)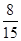 .
.
解析试题分析:(1)先利用频率分布直方图的特点得到第一组和第二组的人数相同,从而得到 的值,然后利用分层抽样中各层的入样比相等求出
的值,然后利用分层抽样中各层的入样比相等求出 的值,最后利用频率、频数以及样本容量三者之间的关系求出
的值,最后利用频率、频数以及样本容量三者之间的关系求出 的值;(2)先确定
的值;(2)先确定 、
、 、
、 组的总人数,然后利用入样比算出每组所抽取的人数;(3)先将各组所抽取的人进行编号,然后列举法找出样本空间以及题中涉及的事件所包含的基本事件及数目,最后利用古典概型的概率计算公式计算事件发生的概率.
组的总人数,然后利用入样比算出每组所抽取的人数;(3)先将各组所抽取的人进行编号,然后列举法找出样本空间以及题中涉及的事件所包含的基本事件及数目,最后利用古典概型的概率计算公式计算事件发生的概率.
试题解析:(1)由频率分布直方图可知,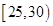 与
与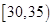 两组的人数相同,所以
两组的人数相同,所以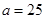 人.
人.
且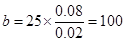 人.总人数
人.总人数 人.
人.
(2)因为第 、
、 、
、 组共有
组共有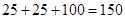 人,利用分层抽样在
人,利用分层抽样在 名员工中抽取
名员工中抽取 人,每组抽取的
人,每组抽取的
人数分别为:
第 组的人数为
组的人数为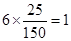 ,第
,第 组的人数为
组的人数为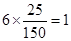 , 第
, 第 组的人数为
组的人数为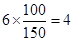 ,
,
所以第 、
、 、
、 组分别抽取
组分别抽取 人,
人, 人,
人,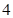 人;
人;
(3)由(2)可设第 组的
组的 人为
人为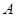 ,第
,第 组的
组的 人为
人为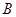 ,第
,第 组的
组的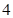 人分别为
人分别为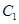 、
、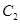 、
、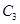 、
、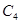 ,则从
,则从
人中抽取 人的所有可能结果为:
人的所有可能结果为: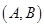 ,
,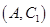 ,
,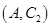 ,
,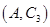 ,
,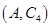 ,
, ,
,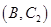 ,
,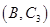 ,
,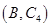 ,
,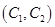 ,
,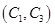 ,
, ,
,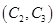 ,
,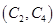 ,
,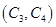 ,共有
,共有 种.
种.
其中恰有 人年龄在第
人年龄在第 组的所有结果为:
组的所有结果为: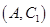 ,
,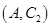 ,
,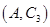 ,
,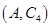 ,
, ,
,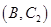 ,
,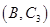 ,
,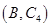 ,共有
,共有 种.
种.
所以恰有 人年龄在第
人年龄在第 组的概率为
组的概率为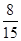 .
.
考点:1.频率分布直方图;2.分层抽样;3.古典概型

练习册系列答案
相关题目
 表示.
表示.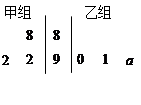
 时,分别从甲、乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值不超过2分的概率.
时,分别从甲、乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值不超过2分的概率.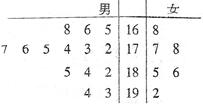

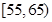 ,
,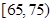 的被调查者中各随机选取1人进行追踪调查,求两人中至少有1人赞成“车辆限行”的概率.
的被调查者中各随机选取1人进行追踪调查,求两人中至少有1人赞成“车辆限行”的概率. 
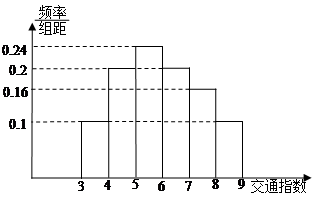

 、第2组
、第2组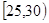 、第3组
、第3组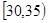 、第4组
、第4组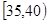 、第5组
、第5组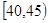 ,得到的频率分布直方图如图所示:
,得到的频率分布直方图如图所示: