题目内容
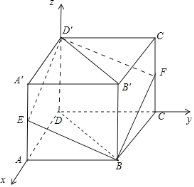
【题目】正方体ABCD﹣A'B'C'D'棱长为2，并且E，F分别是棱AA'，CC'的中点．
（Ⅰ）求证：平面BED'F⊥平面BB'D'D；
（Ⅱ）求直线A'B'与平面BED'F所成的角的正弦值．
【答案】（Ⅰ）证明见解析 （Ⅱ）
【解析】
（Ⅰ））分别以直线DA，DC，DD′为x，y，z轴，建立如图所示的空间直角坐标系，计算平面BED′F的法向量为
，平面BB′D′D的法向量为
，计算
得到证明.
（Ⅱ）计算
，再计算
，得到答案.
（Ⅰ）分别以直线DA，DC，DD′为x，y，z轴，建立如图所示的空间直角坐标系，则：
D（0，0，0），D′（0，0，2），E（2，0，1），B（2，2，0），
∴
，
，
，
设平面BED′F的法向量为
，则：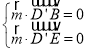
∴
消去x得，y＝x，取x＝1，则得出平面BED′F的一个法向量为，
设平面BB′D′D的法向量为
，则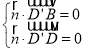
，∴
∴y＝﹣x，取x＝1，则得出平面BB′D′D的一个法向量为，
∵
，∴，
∴平面BED'F⊥平面BB'D'D；
（Ⅱ）∵A′（2，0，2），B′（2，2，2），
∴，且由（Ⅰ）知平面BED'F的法向量，
∴
，
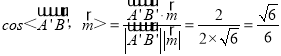∴直线A'B'与平面BED'F所成的角的正弦值为
．
中考解读考点精练系列答案【题目】汽车的普及给人们的出行带来了诸多方便，但汽车超速行驶也造成了诸多隐患.为了解某一段公路汽车通过时的车速情况，现随机抽测了通过这段公路的200辆汽车的时速，所得数据均在区间
中，其频率分布直方图如图所示.
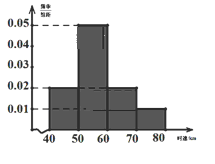
（1）求被抽测的200辆汽车的平均时速.
（2）该路段路况良好，但属于事故高发路段，交警部门对此路段过往车辆限速
.对于超速行驶，交警部门对超速车辆有相应处罚：记分（扣除驾驶员驾照的分数）和罚款.罚款情况如下：
超速情况 | 10%以内 | 10%～20% | 20%～50% | 50%以上 |
罚款情况 | 0元 | 100元 | 150元 | 可以并处吊销驾照 |
①求被抽测的200辆汽车中超速在10%～20%的车辆数.
②该路段车流量比较大，按以前统计该路段每天来往车辆约2000辆.试预估每天的罚款总数.
