题目内容
已知椭圆 (a>b>0)的右焦点为F2(3,0),离心率为
(a>b>0)的右焦点为F2(3,0),离心率为 .
.(1)求椭圆的方程.
(2)设直线y-kx与椭圆相交于A,B两点,M,N分别为线段AF2,BF2的中点,若坐标原点O在以MN为直径的圆上,求k的值.
【答案】分析:(1)由题意得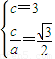 ,解得a,再结合a2=b2+c2,可求得b2,从而可得椭圆的方程;
,解得a,再结合a2=b2+c2,可求得b2,从而可得椭圆的方程;
(2)由椭圆的方程与直线的方程y=kx联立,得(3+12k2)x2-12×3=0,设A(x1,y1),B(x2,y2),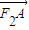 =(x1-3,y1),
=(x1-3,y1),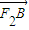 =(x2-3,y2),依题意,AF2⊥BF2,由
=(x2-3,y2),依题意,AF2⊥BF2,由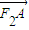 •
•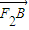 =0即可求得k的值.
=0即可求得k的值.
解答:解:(1)由题意得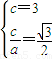 ,得a=2
,得a=2 . …(2分)
. …(2分)
结合a2=b2+c2,解得a2=12,b2=3.…(4分)
所以,椭圆的方程为 +
+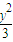 =1. …(6分)
=1. …(6分)
(2)由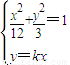 ,得(3+12k2)x2-12×3=0.
,得(3+12k2)x2-12×3=0.
设A(x1,y1),B(x2,y2),
则x1+x2=0,x1x2=-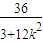 ,…(10分)
,…(10分)
依题意,OM⊥ON,
易知,四边形OMF2N为平行四边形,所以AF2⊥BF2,…(12分)
因为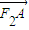 =(x1-3,y1),
=(x1-3,y1),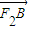 =(x2-3,y2),
=(x2-3,y2),
所以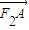 •
•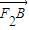 =(x1-3)(x2-3)+y1y2=(1+k2)x1x2+9=0,
=(x1-3)(x2-3)+y1y2=(1+k2)x1x2+9=0,
即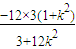 +9=0,
+9=0,
解得k=±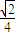 .…(15分)
.…(15分)
点评:本题主要考查椭圆的几何性质,直线与椭圆的位置关系等基础知识,同时考查解析几何的基本思想方法和综合解题能力,属于难题.
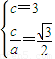 ,解得a,再结合a2=b2+c2,可求得b2,从而可得椭圆的方程;
,解得a,再结合a2=b2+c2,可求得b2,从而可得椭圆的方程;(2)由椭圆的方程与直线的方程y=kx联立,得(3+12k2)x2-12×3=0,设A(x1,y1),B(x2,y2),
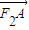 =(x1-3,y1),
=(x1-3,y1),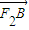 =(x2-3,y2),依题意,AF2⊥BF2,由
=(x2-3,y2),依题意,AF2⊥BF2,由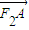 •
•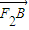 =0即可求得k的值.
=0即可求得k的值.解答:解:(1)由题意得
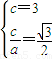 ,得a=2
,得a=2 . …(2分)
. …(2分)结合a2=b2+c2,解得a2=12,b2=3.…(4分)
所以,椭圆的方程为
 +
+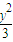 =1. …(6分)
=1. …(6分)(2)由
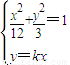 ,得(3+12k2)x2-12×3=0.
,得(3+12k2)x2-12×3=0.设A(x1,y1),B(x2,y2),
则x1+x2=0,x1x2=-
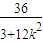 ,…(10分)
,…(10分)依题意,OM⊥ON,
易知,四边形OMF2N为平行四边形,所以AF2⊥BF2,…(12分)
因为
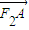 =(x1-3,y1),
=(x1-3,y1),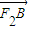 =(x2-3,y2),
=(x2-3,y2),所以
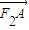 •
•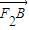 =(x1-3)(x2-3)+y1y2=(1+k2)x1x2+9=0,
=(x1-3)(x2-3)+y1y2=(1+k2)x1x2+9=0,即
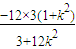 +9=0,
+9=0,解得k=±
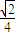 .…(15分)
.…(15分)点评:本题主要考查椭圆的几何性质,直线与椭圆的位置关系等基础知识,同时考查解析几何的基本思想方法和综合解题能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
 =2
=2 ,
, ·
· =
= ,求椭圆的方程.
,求椭圆的方程. (a>b>0),点
(a>b>0),点 在椭圆上。
在椭圆上。 (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆 有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B. 分)
分) (a>b>0)的离心率
(a>b>0)的离心率 ,焦距是函数
,焦距是函数 的零点.
的零点. 与椭圆交于
与椭圆交于 、
、 两点,
两点, ,求k的值.
,求k的值.