题目内容
设m∈R,在平面直角坐标系中,已知向量a=(mx,y+1),向量b=(x,y-1),a⊥b,动点M(x,y)的轨迹为E.(Ⅰ)求轨迹E的方程,并说明该方程所表示曲线的形状;
(Ⅱ)已知m=
 .证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点),并求该圆的方程;
.证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点),并求该圆的方程;(Ⅲ)已知m=
 .设直线l与圆C:x2+y2=R2(1<R<2)相切于A1,且l与轨迹E只有一个公共点B1.当R为何值时,|A1B1|取得最大值?并求最大值.
.设直线l与圆C:x2+y2=R2(1<R<2)相切于A1,且l与轨迹E只有一个公共点B1.当R为何值时,|A1B1|取得最大值?并求最大值.
【答案】分析:(1)由a⊥b,所以a•b=0,代入坐标化简整理即得轨迹E的方程mx2+y2=1.
此为二元二次曲线,可分m=0、m=1、m>0且m≠1和m<0四种情况讨论;
(2)当m= 时,轨迹E的方程为
时,轨迹E的方程为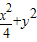 =1,表示椭圆,设圆的方程为x2+y2=r2(0<r<1),
=1,表示椭圆,设圆的方程为x2+y2=r2(0<r<1),
当切线斜率存在时,可设圆的任一切线方程为y=kx+t,由直线和圆相切可得k和t的关系,
由OA⊥OB,所以x1x2+y1y1=0,只需联立直线和圆的方程,消元,维达定理,又可以得到k和t的关系,这样就可解出r.
当切线斜率不存在时,代入检验即可.
(3)因为l与圆C相切,故△OA1B1为直角△,故|A1B1|2=|OB1|2-|OA1|2,只需求出OB1和OA1的长度即可,
直线l与圆C相切,且与椭圆相切找出关系,将|A1B1|表示为R的函数,转化为函数求最值.
解答:解:(Ⅰ)因为a⊥b,
所以a•b=0,即(mx,y+1)•(x,y-1)=0,
故mx2+y2-1=0,即mx2+y2=1.
当m=0时,该方程表示两条直线;
当m=1时,该方程表示圆;
当m>0且m≠1时,该方程表示椭圆;
当m<0时,该方程表示双曲线.
(Ⅱ)当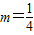 时,轨迹E的方程为
时,轨迹E的方程为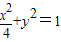 ,
,
设圆的方程为x2+y2=r2(0<r<1),当
切线斜率存在时,可设圆的任一切线方程为y=kx+t,
A(x1,y1),B(x2,y2),
所以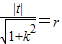 ,
,
即t2=r2(1+k2).①
因为OA⊥OB,
所以x1x2+y1y1=0,
即x1x2+(kx1+t)(kx2+t)=0,
整理得(1+k2)x1x2+kt(x1+x2)+t2=0.②
由方程组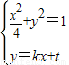
消去y得
(1+4k2)x2+8ktx+4t2-4=0.③
由韦达定理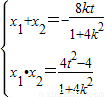
代入②式并整理得
(1+k2)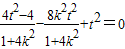 ,
,
即5t2=4+4k2.
结合①式有5r2=4,r=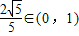 ,
,
当切线斜率不存在时,x2+y2= 也满足题意,
也满足题意,
故所求圆的方程为x2+y2= .
.
(Ⅲ)显然,直线l的斜率存在,
设l的方程y=k1x+t1,B1(x3,y3)
轨迹E的方程为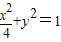 .
.
由直线l与圆相切得t12=R2(1+k12),
且对应③式有△=(8k1t1)2-4(1+4k12)(4t12-4)=0,
即t12=1+4k12,
由方程组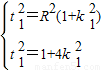 ,
,
解得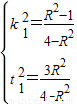
当l与轨迹E只有一个公共点时,对应的方程③应有两个相等的.
由韦达定理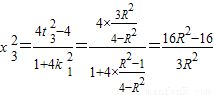 ,
,
又B1在椭圆上,
所以 ,
,
因为l与圆C相切,
所以|A1B1|2=|OB1|2-|OA1|2=x32+y32-R2
=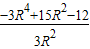
=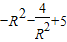
=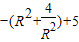 ≤
≤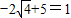 ,
,
其中,等号成立的条件
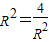 ,
,
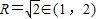 .
.
即故当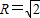 时,|A1B1|的最大值为1.
时,|A1B1|的最大值为1.
点评:本题考查求轨迹方程、及方程所表示的曲线、直线与圆、直线与椭圆的位置关系等知识,考查计算能力和分析问题解决问题的能力,综合性强,难度较大.
此为二元二次曲线,可分m=0、m=1、m>0且m≠1和m<0四种情况讨论;
(2)当m=
 时,轨迹E的方程为
时,轨迹E的方程为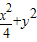 =1,表示椭圆,设圆的方程为x2+y2=r2(0<r<1),
=1,表示椭圆,设圆的方程为x2+y2=r2(0<r<1),当切线斜率存在时,可设圆的任一切线方程为y=kx+t,由直线和圆相切可得k和t的关系,
由OA⊥OB,所以x1x2+y1y1=0,只需联立直线和圆的方程,消元,维达定理,又可以得到k和t的关系,这样就可解出r.
当切线斜率不存在时,代入检验即可.
(3)因为l与圆C相切,故△OA1B1为直角△,故|A1B1|2=|OB1|2-|OA1|2,只需求出OB1和OA1的长度即可,
直线l与圆C相切,且与椭圆相切找出关系,将|A1B1|表示为R的函数,转化为函数求最值.
解答:解:(Ⅰ)因为a⊥b,
所以a•b=0,即(mx,y+1)•(x,y-1)=0,
故mx2+y2-1=0,即mx2+y2=1.
当m=0时,该方程表示两条直线;
当m=1时,该方程表示圆;
当m>0且m≠1时,该方程表示椭圆;
当m<0时,该方程表示双曲线.
(Ⅱ)当
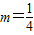 时,轨迹E的方程为
时,轨迹E的方程为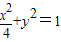 ,
,设圆的方程为x2+y2=r2(0<r<1),当
切线斜率存在时,可设圆的任一切线方程为y=kx+t,
A(x1,y1),B(x2,y2),
所以
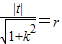 ,
,即t2=r2(1+k2).①
因为OA⊥OB,
所以x1x2+y1y1=0,
即x1x2+(kx1+t)(kx2+t)=0,
整理得(1+k2)x1x2+kt(x1+x2)+t2=0.②
由方程组
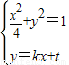
消去y得
(1+4k2)x2+8ktx+4t2-4=0.③
由韦达定理
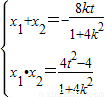
代入②式并整理得
(1+k2)
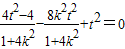 ,
,即5t2=4+4k2.
结合①式有5r2=4,r=
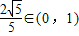 ,
,当切线斜率不存在时,x2+y2=
 也满足题意,
也满足题意,故所求圆的方程为x2+y2=
 .
.(Ⅲ)显然,直线l的斜率存在,
设l的方程y=k1x+t1,B1(x3,y3)
轨迹E的方程为
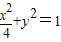 .
.由直线l与圆相切得t12=R2(1+k12),
且对应③式有△=(8k1t1)2-4(1+4k12)(4t12-4)=0,
即t12=1+4k12,
由方程组
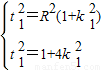 ,
,解得
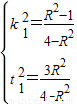
当l与轨迹E只有一个公共点时,对应的方程③应有两个相等的.
由韦达定理
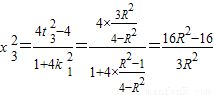 ,
,又B1在椭圆上,
所以
 ,
,因为l与圆C相切,
所以|A1B1|2=|OB1|2-|OA1|2=x32+y32-R2
=
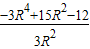
=
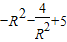
=
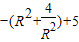 ≤
≤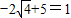 ,
,其中,等号成立的条件
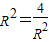 ,
,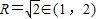 .
.即故当
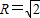 时,|A1B1|的最大值为1.
时,|A1B1|的最大值为1.点评:本题考查求轨迹方程、及方程所表示的曲线、直线与圆、直线与椭圆的位置关系等知识,考查计算能力和分析问题解决问题的能力,综合性强,难度较大.

练习册系列答案
相关题目