题目内容
(2013•天河区三模)设m∈R,在平面直角坐标系中,已知向量
=(x+
,my),向量
=(x-
,y),
⊥
,动点M(x,y)的轨迹为曲线E.
(I)求曲线E的方程,并说明该方程所表示曲线的形状;
(II) 已知m=
,F(0,-1),直线l:y=kx+1与曲线E交于不同的两点M、N,则△FMN的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的实数k的值;若不存在,请说明理由.
| a |
| 3 |
| b |
| 3 |
| a |
| b |
(I)求曲线E的方程,并说明该方程所表示曲线的形状;
(II) 已知m=
| 3 |
| 4 |
分析:(Ⅰ)直接由向量数量积的坐标表示得到动点M(x,y)的轨迹,然后对m的取值分类讨论,得到曲线E的不同形状;
(Ⅱ)把m=
代入曲线E的方程,求出具体的椭圆方程,由直线系方程知直线l过椭圆的上焦点,则△FMN的周长为定值,设△FMN的内切圆半径为r,把三角形的面积用r表示,可知当△FMN的面积最大时其内切圆半径最大,联立直线方程和椭圆方程,把△FMN的面积用含有k的代数式表示,换元后利用导数求△FMN的最大值,进一步求出r的最大值,则△FMN的内切圆的面积的最大值可求.
(Ⅱ)把m=
| 3 |
| 4 |
解答:解:(Ⅰ)
=(x+
,my),向量
=(x-
,y),
因为
•
,所以
•
=x2+my2-3=0,即x2+my2=3.
当m=0时,方程表示两直线,方程为x=±
;
当m=1时,方程表示的是以原点为圆心,以
为半径的圆;
当0<m<1时,方程表示焦点在y轴上的椭圆,当m>1时,方程表示焦点在x轴上的椭圆;
当m<0时,方程表示焦点在x轴上的双曲线.
(Ⅱ)当m=
时,曲线E的方程为椭圆
+
=1,F(0,-1)为椭圆的下焦点,
直线l:y=kx+1过椭圆的上焦点F'(0,1),则△FMN的周长等于4a=8,
设△FMN的内切圆的径r,
则S△FMN=
(MN+FM+FN)r=4r,因此,若S△FMN最大,r就最大,
设M(x1,y1),N(x2,y2),不妨x1>0,x2<0,SAMN=
|FF′|(x1-x2)=x1-x2,
由
,得(3k2+4)x2+6kx-9=0
得x1=
,x2=
,
则S△FMN=
|FF′|•(x1-x2)=x1-x2=
,
令t=
,则t≥1,
则S△FMN=
=
=
,
令f(t)=3t+
,则f′(t)=3-
,
当t≥1时,f′(t)≥0,f(t)在[1,+∞)上单调递增,
有f(t)≥f(1)=4,所以S△FMN≤
=3,
即当t=1,k=0时,S△FMN≤
=3,
由S△FMN=4r=3,∴rmax=
,
这时所求内切圆面积的最大值为πr2=π×(
)2=
π.
故k=0,△AMN内切圆面积的最大值为
π.
| a |
| 3 |
| b |
| 3 |
因为
| a |
| b |
| a |
| b |
当m=0时,方程表示两直线,方程为x=±
| 3 |
当m=1时,方程表示的是以原点为圆心,以
| 3 |
当0<m<1时,方程表示焦点在y轴上的椭圆,当m>1时,方程表示焦点在x轴上的椭圆;
当m<0时,方程表示焦点在x轴上的双曲线.
(Ⅱ)当m=
| 3 |
| 4 |
| y2 |
| 4 |
| x2 |
| 3 |
直线l:y=kx+1过椭圆的上焦点F'(0,1),则△FMN的周长等于4a=8,
设△FMN的内切圆的径r,
则S△FMN=
| 1 |
| 2 |
设M(x1,y1),N(x2,y2),不妨x1>0,x2<0,SAMN=
| 1 |
| 2 |
由
|
得x1=
-3k+6
| ||
| 3k2+4 |
-3k-6
| ||
| 3k2+4 |
则S△FMN=
| 1 |
| 2 |
12
| ||
| 3k2+4 |
令t=
| k2+1 |
则S△FMN=
12
| ||
| 3k2+4 |
| 12t |
| 3t2+1 |
| 12 | ||
3t+
|
令f(t)=3t+
| 1 |
| t |
| 1 |
| t2 |
当t≥1时,f′(t)≥0,f(t)在[1,+∞)上单调递增,
有f(t)≥f(1)=4,所以S△FMN≤
| 12 |
| 4 |
即当t=1,k=0时,S△FMN≤
| 12 |
| 4 |
由S△FMN=4r=3,∴rmax=
| 3 |
| 4 |
这时所求内切圆面积的最大值为πr2=π×(
| 3 |
| 4 |
| 9 |
| 16 |
故k=0,△AMN内切圆面积的最大值为
| 9 |
| 16 |
点评:本题考查了轨迹方程的求法,考查了平面向量数量积的坐标运算,考查了直线与圆锥曲线的关系,运用了分类讨论的数学思想方法和数学转化思想方法,考查了换元法和利用导数求函数的最值,是有一定难度题目.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
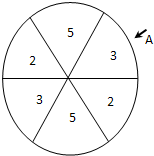 (2013•天河区三模)如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(a,b)(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).
(2013•天河区三模)如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(a,b)(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).