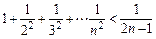题目内容
已知下列方程(1) ,(2)
,(2) ,(3)
,(3) 中至少有一个方程有实根,求实数
中至少有一个方程有实根,求实数 的取值范围.
的取值范围.
 ,(2)
,(2) ,(3)
,(3) 中至少有一个方程有实根,求实数
中至少有一个方程有实根,求实数 的取值范围.
的取值范围.
试题分析:采用“正难则反”的思想方法处理,假设三个方程都没有实数根,
则
 由此解得
由此解得 ,
,从而三个方程至少有一个有实数根时,实数
 的取值范围是
的取值范围是 .
.点评:解决的关键是根据反设,得到结论的否定形式,然后在假设的基础上推理论证,属于基础题

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
 是f(x)=0的一个根;
是f(x)=0的一个根; =1写出具有类似特性的性质,并加以证明.
=1写出具有类似特性的性质,并加以证明. >0,
>0, >0,
>0, >0,用反证法求证
>0,用反证法求证 >0,
>0,  >0,c>0的假设为
>0,c>0的假设为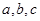 不全是正数
不全是正数 <
<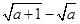 ,其中a≥0.=
,其中a≥0.=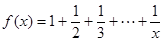 ,计算得当
,计算得当 时
时 ,当
,当 时有
时有 ,
, ,
, ,
, ,因此猜测当
,因此猜测当 ,
, ,
, 中至少有一个不小于2”时的假设为_ _____
中至少有一个不小于2”时的假设为_ _____  ,…,可归纳出式子( )
,…,可归纳出式子( )