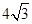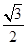题目内容
与椭圆C: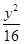 +
+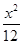 =1共焦点且过点(1,
=1共焦点且过点(1, )的双曲线的标准方程为( )
)的双曲线的标准方程为( )
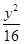 +
+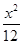 =1共焦点且过点(1,
=1共焦点且过点(1, )的双曲线的标准方程为( )
)的双曲线的标准方程为( )A.x2-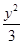 =1 =1 | B.y2-2x2=1 |
C. - -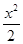 =1 =1 | D.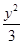 -x2=1 -x2=1 |
C
椭圆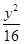 +
+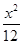 =1的焦点坐标为(0,-2),(0,2).设双曲线的标准方程为
=1的焦点坐标为(0,-2),(0,2).设双曲线的标准方程为 -
-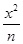 =1(m>0,n>0),则
=1(m>0,n>0),则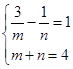 解得m=n=2.
解得m=n=2.
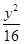 +
+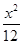 =1的焦点坐标为(0,-2),(0,2).设双曲线的标准方程为
=1的焦点坐标为(0,-2),(0,2).设双曲线的标准方程为 -
-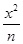 =1(m>0,n>0),则
=1(m>0,n>0),则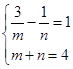 解得m=n=2.
解得m=n=2.
练习册系列答案
相关题目
 、抛物线
、抛物线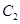 的焦点均在
的焦点均在 轴上,
轴上,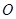 ,从每条曲线上取两个点,将其坐标记录如下:
,从每条曲线上取两个点,将其坐标记录如下: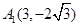 、
、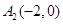 、
、 、
、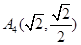 .
.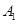 ,
, 在抛物线
在抛物线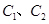 的标准方程;
的标准方程;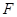 的坐标并求出椭圆
的坐标并求出椭圆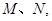 且满足
且满足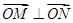 ,试求出直线的方程.
,试求出直线的方程. )且斜率为k的直线l与椭圆
)且斜率为k的直线l与椭圆 +y2=1有两个不同的交点P和Q.
+y2=1有两个不同的交点P和Q. +
+ 与
与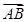 共线?如果存在,求k的值;如果不存在,请说明理由.
共线?如果存在,求k的值;如果不存在,请说明理由. 连线的斜率的积为定值
连线的斜率的积为定值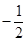 .
. 与曲线C交于M、N两点,当|MN|=
与曲线C交于M、N两点,当|MN|=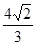 时,求直线l的方程.
时,求直线l的方程. 的椭圆
的椭圆 的两个顶点分别为
的两个顶点分别为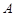 和
和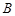 ,且
,且 与n
与n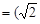 ,
,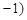 共线.
共线.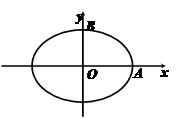
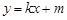 与椭圆
与椭圆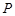 和
和 ,且原点
,且原点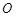 总在以
总在以 为直径的圆的内部,求实数
为直径的圆的内部,求实数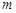 的取值范围.
的取值范围. 右支上的一点,M,N分别是圆(x+5)2+y2=4和(x-5)2+y2=1上的点,则|PM|-|PN|的最大值为( )
右支上的一点,M,N分别是圆(x+5)2+y2=4和(x-5)2+y2=1上的点,则|PM|-|PN|的最大值为( ) ,
, 为小圆上的一条定直径,则以大圆的切线为准线,且过
为小圆上的一条定直径,则以大圆的切线为准线,且过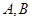 两点的抛物线焦点
两点的抛物线焦点 的轨迹方程为( )(以线段
的轨迹方程为( )(以线段 轴,其中垂线为
轴,其中垂线为 轴建立平面直角坐标系)
轴建立平面直角坐标系)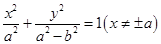

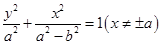

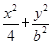 =1(0<b<2)与y轴交于A,B两点,点F为该椭圆的一个焦点,则△ABF面积的最大值为________.
=1(0<b<2)与y轴交于A,B两点,点F为该椭圆的一个焦点,则△ABF面积的最大值为________.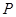 是椭圆上的一点,
是椭圆上的一点,  是焦点, 且, 则△
是焦点, 且, 则△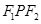 的面积是
的面积是