题目内容
已知函数
(I)求函数 的单调增区间;
的单调增区间;
(II)当 时,求函数
时,求函数 的最大值及相应的
的最大值及相应的 值.
值.
(I) 的单调递增区间为
的单调递增区间为
(II)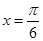 时.
时.  取最大值,最大值为2.
取最大值,最大值为2.
解析试题分析:(I)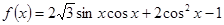
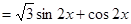
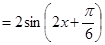
令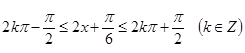 得
得
∴ 的单调递增区间为
的单调递增区间为
(II)由 可得
可得
所以当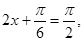 即
即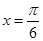 时.
时.  取最大值,最大值为2.
取最大值,最大值为2.
考点:本题主要考查三角函数的和差倍半公式,三角函数的图象和性质。
点评:中档题,本题综合考查三角函数的和差倍半公式,三角函数的图象和性质。运用三角公式对三角函数式进行化简,以便于进一步研究函数的性质,是这类题的显著特点。

练习册系列答案
相关题目
 的最大值为3,其图像相邻两条对称轴之间的距离为
的最大值为3,其图像相邻两条对称轴之间的距离为
 的解析式
的解析式 ,则
,则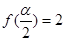 ,求
,求 的值
的值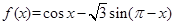 .
.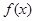 的最小正周期和值域;
的最小正周期和值域;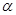 是第二象限角,且
是第二象限角,且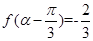 ,试求
,试求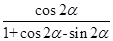 的值.
的值. .
. 的最小正周期和值域;
的最小正周期和值域; ,求
,求 的值.
的值.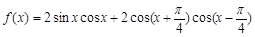 。
。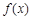 的单调递减区间; (2)设
的单调递减区间; (2)设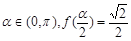 ,求
,求 的值。
的值。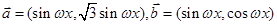 (
( ),函数
),函数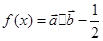 ,且
,且 的最小正周期为
的最小正周期为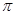 .
. 的值;
的值; (
( )的部分图像如右所示.
)的部分图像如右所示.
 的解析式;
的解析式; ,且
,且 ,求
,求 的值.
的值. 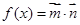 其中,
其中,
 的最小正周期及单调减区间.
的最小正周期及单调减区间. 的两根为sinθ和cosθ:
的两根为sinθ和cosθ: 的值;
的值;