Question

【题目】已知f(x)是定义在R上的偶函数，且x≤0时，f(x)＝log (－x＋1)．

(1)求f(0)，f(1)；

(2)求函数f(x)的解析式；

(3)若f(a－1)<－1，求实数a的取值范围．

Answer 1

【答案】（1）f(0)＝0，f(1)＝－1；（2）；（3）(－∞，0)∪(2，＋∞).

【解析】试题分析：（1）代入x的值，求出函数值即可；
（2）根据函数的奇偶性求出函数的解析式即可；
（3）通过讨论a的范围，得到关于a的不等式，解出即可．

试题解析：

(1)因为当x≤0时，f(x)＝log (－x＋1)，

所以f(0)＝0.

又因为函数f(x)是定义在R上的偶函数，

所以f(1)＝f(－1)＝log [－(－1)＋1]＝log2＝－1，

即f(1)＝－1.

(2)令x>0，则－x<0，

从而f(－x)＝log (x＋1)＝f(x)，

∴x>0时，f(x)＝log (x＋1)．

∴函数f(x)的解析式为f(x)＝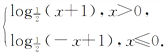

(3)设x1，x2是任意两个值，且x1<x2≤0，

则－x1>－x2≥0，

∴1－x1>1－x2>0.

∵f(x2)－f(x1)＝log (－x2＋1)－log (－x1＋1)＝log>log1＝0，

∴f(x2)>f(x1)，

∴f(x)＝log (－x＋1)在(－∞，0]上为增函数．

又∵f(x)是定义在R上的偶函数，

∴f(x)在(0，＋∞)上为减函数．

∵f(a－1)<－1＝f(1)，

∴|a－1|>1，解得a>2或a<0.

故实数a的取值范围为(－∞，0)∪(2，＋∞)．

点睛: 本题考查利用函数的奇偶性求函数解析式,判断并证明函数的单调性,属于中档题目.证明函数单调性的一般步骤：（1）取值：在定义域上任取，并且（或）；（2）作差： ，并将此式变形（要注意变形到能判断整个式子符号为止）；（3）定号；（4）下结论.