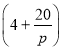题目内容
【题目】已知四棱锥![]() 的底面为正方形,且该四棱锥的每条棱长均为
的底面为正方形,且该四棱锥的每条棱长均为![]() ,设BC,CD的中点分别为E,F,点G在线段PA上,如图.
,设BC,CD的中点分别为E,F,点G在线段PA上,如图.
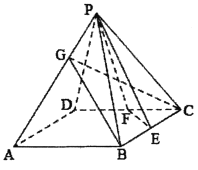
(1)证明:![]() ;
;
(2)当![]() 平面PEF时,求直线GC和平面PEF所成角的正弦值.
平面PEF时,求直线GC和平面PEF所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)设![]() ,由正棱锥的性质可知PO⊥平面ABCD,得到PO⊥EF,再由ABCD是正方形结合EF为△BCD的中位线,可得EF⊥AC,得到EF⊥平面PAC,进一步得到EF⊥GC;
,由正棱锥的性质可知PO⊥平面ABCD,得到PO⊥EF,再由ABCD是正方形结合EF为△BCD的中位线,可得EF⊥AC,得到EF⊥平面PAC,进一步得到EF⊥GC;
(2)分别以PB,OC,OP为x,y,z轴建立空间直角坐标系,求出A,P,E,F的坐标,设![]() ,且
,且![]() ,其中
,其中![]() ,求得
,求得![]() ,设平面PEF的一个法向量为
,设平面PEF的一个法向量为![]() ,求得
,求得![]() ,结合BG∥平面PEF,利用数量积为0求得λ,进一步得到
,结合BG∥平面PEF,利用数量积为0求得λ,进一步得到![]() ,又
,又![]() ,求出直线GC的法向量为
,求出直线GC的法向量为![]() .设GC和平面PEF所成角为
.设GC和平面PEF所成角为![]() ,再由
,再由![]() 求解.
求解.
(1)证明:由已知![]() 为正四棱锥,设AC,BD交于点O,
为正四棱锥,设AC,BD交于点O,
由正棱锥的性质可知![]() 平面ABCD,所以
平面ABCD,所以![]() ,
,
由于正方形ABCD满足![]() ,EF为
,EF为![]() 的中位线,故
的中位线,故![]() ,所以
,所以![]() ,
,
所以![]() 平面PAC,而
平面PAC,而![]() 平面PAC,所以
平面PAC,所以![]() .
.
(2)分别以OB,OC,OP为坐标轴建立如图坐标系,
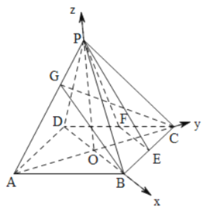
此时![]() ,
,![]() ,
,![]() ,
,![]() .
.
设![]() ,且
,且![]() ,其中
,其中![]() ,
,
即![]() ,
,
设平面PEF的法向量为![]() ,
,
由于![]() ,
,![]() ,
,
由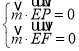 解得
解得![]() ,
,
由![]() 平面PEF知
平面PEF知![]() ,
,
解得![]() ,此时
,此时![]() ,由于
,由于![]() ,故
,故![]() .
.
所以直线GC的方向向量![]() ,
,
设GC和平面PEF所成角为![]() ,
,
则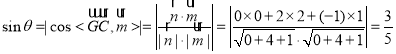 .
.

【题目】如图,在四棱锥P﹣ABCD中,侧面PAD⊥底面ABCD,∠PAD=90°,CD∥AB,∠BAD=90°,且AB=3CD=3PA![]() AD=3.
AD=3.
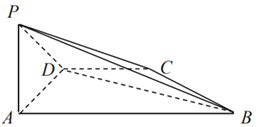
(1)求证:BD⊥PC;
(2)求点A到平面PCD的距离.
【题目】某工厂因排污比较严重,决定着手整治,一个月时污染度为![]() ,整治后前四个月的污染度如下表:
,整治后前四个月的污染度如下表:
月数 |
|
|
|
| … |
污染度 |
|
|
|
| … |
污染度为![]() 后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:
后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:![]() ,
,![]() ,
,![]() ,其中
,其中![]() 表示月数,
表示月数,![]() 、
、![]() 、
、![]() 分别表示污染度.
分别表示污染度.
(1)问选用哪个函数模拟比较合理,并说明理由;
(2)若以比较合理的模拟函数预测,整治后有多少个月的污染度不超过![]() .
.